Spherical coordinates
Spherical coordinates can be a little challenging to understand at first. Spherical coordinates determine the position of a point in three-dimensional space based on the distance $\rho$ from the origin and two angles $\theta$ and $\phi$. If one is familiar with polar coordinates, then the angle $\theta$ isn't too difficult to understand as it is essentially the same as the angle $\theta$ from polar coordinates. But some people have trouble grasping what the angle $\phi$ is all about.
The following graphics and interactive applets may help you understand spherical coordinates better. On this page, we derive the relationship between spherical and Cartesian coordinates, show an applet that allows you to explore the influence of each spherical coordinate, and illustrate simple spherical coordinate surfaces.
Relationship between spherical and Cartesian coordinates
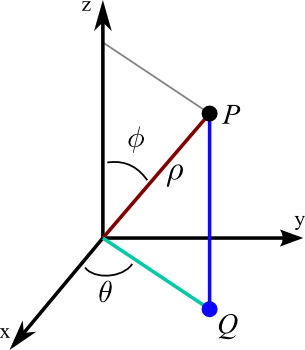
Spherical coordinates are defined as indicated in the following figure, which illustrates the spherical coordinates of the point $P$.
The coordinate $\rho$ is the distance from $P$ to the origin. If the point $Q$ is the projection of $P$ to the $xy$-plane, then $\theta$ is the angle between the positive $x$-axis and the line segment from the origin to $Q$. Lastly, $\phi$ is the angle between the positive $z$-axis and the line segment from the origin to $P$.
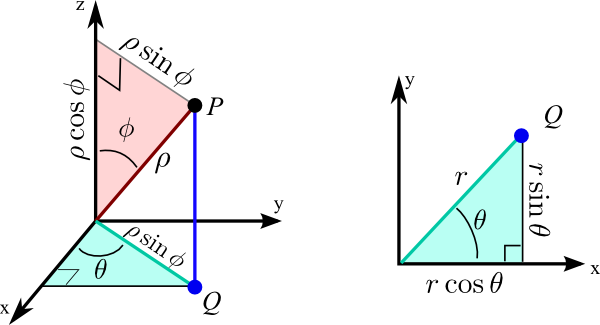
We can calculate the relationship between the Cartesian coordinates $(x,y,z)$ of the point $P$ and its spherical coordinates $(\rho,\theta,\phi)$ using trigonometry. The pink triangle above is the right triangle whose vertices are the origin, the point $P$, and its projection onto the $z$-axis. As the length of the hypotenuse is $\rho$ and $\phi$ is the angle the hypotenuse makes with the $z$-axis leg of the right triangle, the $z$-coordinate of $P$ (i.e., the height of the triangle) is $z=\rho\cos\phi$. The length of the other leg of the right triangle is the distance from $P$ to the $z$-axis, which is $r=\rho\sin\phi$. The distance of the point $Q$ from the origin is the same quantity.
The cyan triangle, shown in both the original 3D coordinate system on the left and in the $xy$-plane on the right, is the right triangle whose vertices are the origin, the point $Q$, and its projection onto the $x$-axis. In the right plot, the distance from $Q$ to the origin, which is the length of hypotenuse of the right triangle, is labeled just as $r$. As $\theta$ is the angle this hypotenuse makes with the $x$-axis, the $x$- and $y$-components of the point $Q$ (which are the same as the $x$- and $y$-components of the point $P$) are given by $x=r\cos\theta$ and $y=r\sin\theta$. Since $r=\rho\sin\phi$, these components can be rewritten as $x=\rho\sin\phi\cos\theta$ and $y=\rho\sin\phi\sin\theta$. In summary, the formulas for Cartesian coordinates in terms of spherical coordinates are \begin{align} x &= \rho\sin\phi\cos\theta\notag\\ y &= \rho\sin\phi\sin\theta\label{spherical_cartesian}\tag{1}\\ z &= \rho\cos\phi\notag. \end{align}
Exploring the influence of each spherical coordinate
The below applet allows you to see how the location of a point changes as you vary $\rho$, $\theta$, and $\phi$. The point $P$ corresponding to the value of the coordinates is shown as a large purple point. The green dot is the point $Q$, i.e., the projection of $P$ in the $xy$-plane.
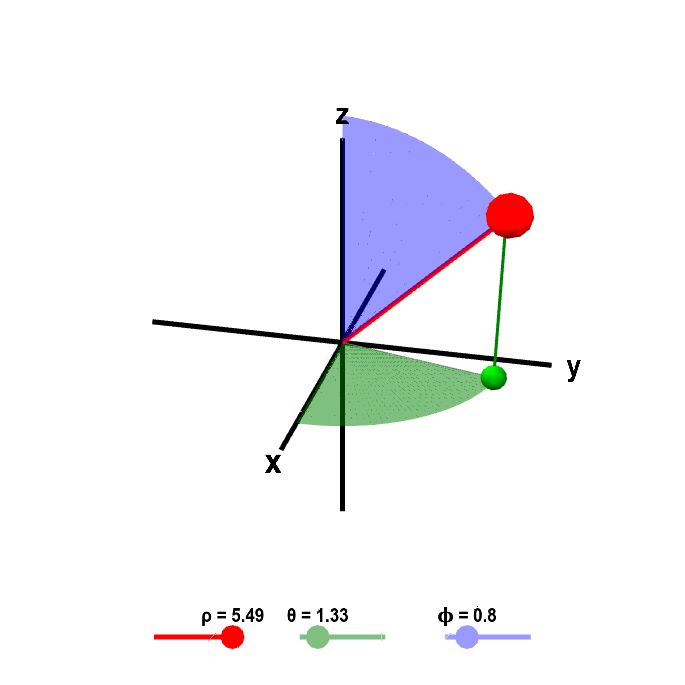
Applet loading
Spherical coordinates. Given the values for spherical coordinates $\rho$, $\theta$, and $\phi$, which you can change by dragging the points on the sliders, the large red point shows the corresponding position in Cartesian coordinates. The green dot is the projection of the point in the $xy$-plane. You can visualize each of the spherical coordinates by the geometric structures that are colored corresponding to the slider colors. The length of the red line segment from the origin is $\rho$. The angle of the green portion of the disk in the $xy$-plane is $\theta$. The angle of the blue portion of the vertical disk is $\phi$. You can also move the large red point and the green projection of that point directly with the mouse.
Notice how you can obtain any point even though we restrict $\rho \ge 0$, $0 \le \theta < 2\pi$, and $0 \le \phi \le \pi$. Can you see why we only need $\phi$ to go up to $\pi$?
These restrictions removed much of the non-uniqueness of spherical coordinates. Notice there is still non-uniqueness at $\rho =0$, at $\phi = 0$ and at $\phi=\pi$. When any of these conditions are true, you can change the value of one or more of the other coordinates without moving the point.
Unfortunately, the convention for the notation of spherical coordinates is not standardized across disciplines. For example, in physics, the roles of $\theta$ and $\phi$ are typically reversed. In order to correctly understand someone's use of spherical coordinates, you must first determine what notational convention this are using. You cannot assume they follow the convention used here.
Simple spherical coordinate surfaces
These three next applets may help you understand what each of three spherical coordinates means. They show what the surfaces $\phi=$ constant, $\theta=$ constant, and $\rho=$ constant look like. The value of the constant is determined by the position of the sliders. In all cases, we restrict the surfaces to the region $\rho <5$.
Constant $\phi$
What does it mean for a point to have the spherical coordinate $\phi=\pi/3$? Take a look at the surfaces that are defined by the equation $\phi=$ constant.
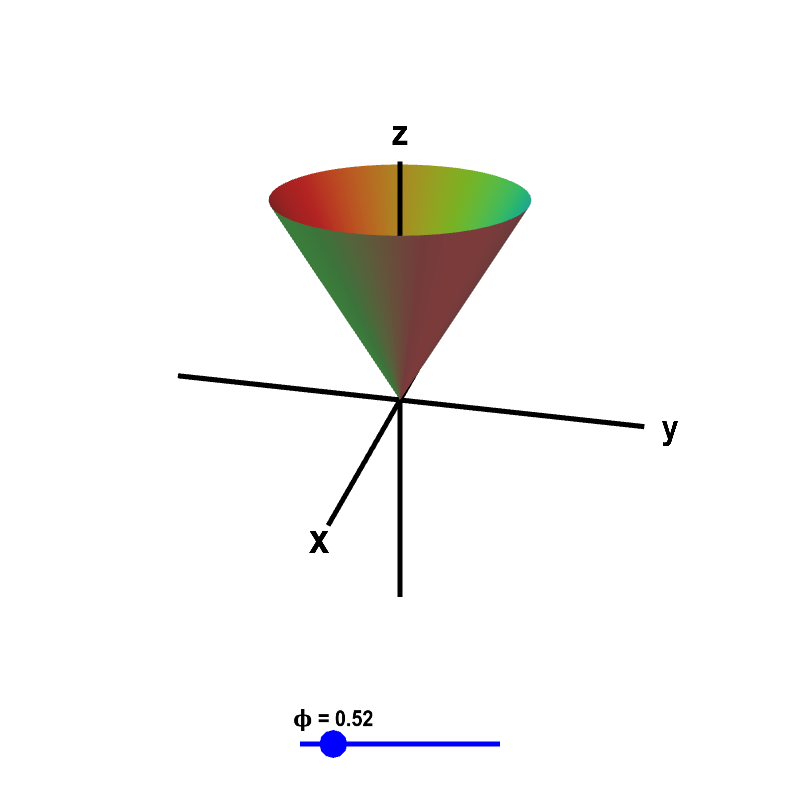
Applet loading
Surfaces of constant $\phi$ in spherical coordinates. The conical surface of $\phi=$ constant is shown, where the value of $\phi$ is determined by the blue point on the slider. Only the part of the surface where $\rho < 5$ is shown.
The surface $\phi=$ constant is simply a single cone, pointing either upward or downward. If you know that $\phi=\pi/3$, then you know the point is somewhere on a (wide) single cone that opens upward, i.e., the equation $\phi=\pi/3$ specifies a surface that is a single cone opening upward. The equation $\phi=\pi/2$ corresponds to the $xy$-plane.
The surface $\phi=$ constant is rotationally symmetric around the $z$-axis. Therefore it must depend on $x$ and $y$ only via the distance $\sqrt{x^2+y^2}$ from the $z$-axis. Using the relationship \eqref{spherical_cartesian} between spherical and Cartesian coordinates, one can calculate that \begin{align*} x^2+y^2 &= \rho^2\sin^2\phi(\cos^2\theta + \sin^2\theta)\\ &= \rho^2\sin^2\phi \end{align*} or $\sqrt{x^2+y^2} = \rho\sin\phi$. (Given that $0 \le \phi \le \pi$, we know that $\sin \phi \ge 0$ and the positive square root is $\rho\sin\phi$.) If we divide by $z=\rho\cos\phi$, we obtain a formula for $\phi$ in terms of Cartesian coordinates $$\frac{\sqrt{x^2+y^2}}{z} = \tan \phi.$$ We can rewrite the surface $\phi=$ constant as $$z = C \sqrt{x^2+y^2}$$ where $C=1/\tan \phi$, which is indeed the equation for a cone.
Constant $\theta$
The surface $\theta=$ constant is a half-plane off the $z$-axis. (It is plotted as a half-disk only because we restrict the plot to $\rho<5$.)
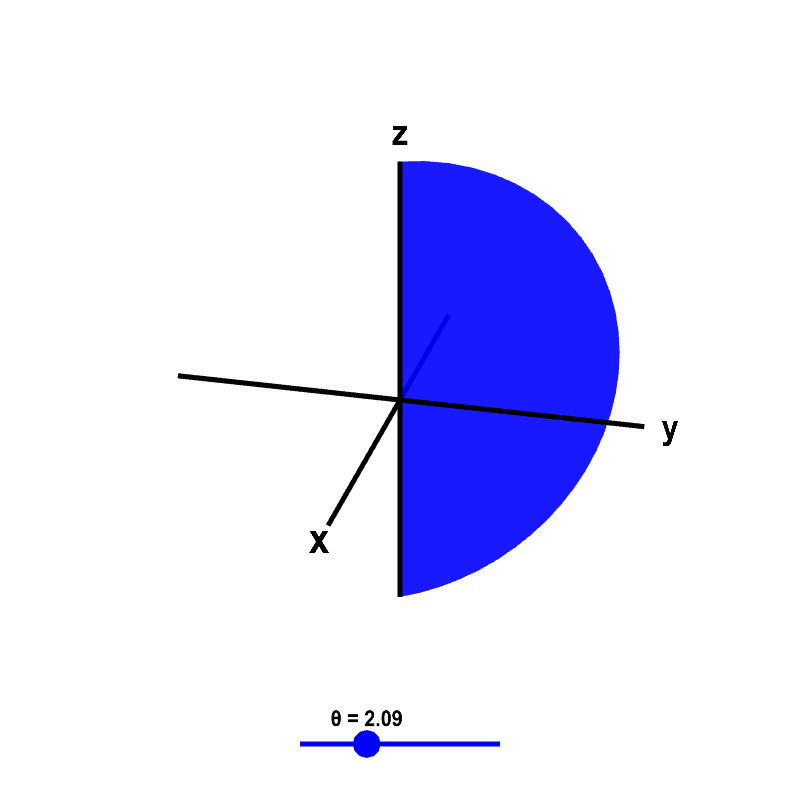
Applet loading
Surfaces of constant $\theta$ in spherical coordinates. The half-plane surface of $\theta=$ constant is shown, where the value of $\theta$ is determined by the blue point on the slider. Only the part of the surface where $\rho < 5$ is shown, which makes the half-plane appear like a half-disk.
If a point has $\theta=\pi/2$, then you know the point is on the half of the $yz$-plane where $y$ values are positive. The equation $\theta=\pi/2$ is the equation for this half-plane.
From relationship \eqref{spherical_cartesian}, the ratio between $x$ and $y$ can be written, for example, as $y/x = \tan \theta$. If $\theta$ is held constant, then the ratio between $x$ and $y$ is constant. Thus, the equation $\theta=$ constant gives a line through the origin in the $xy$-plane. Since $z$ is unrestricted, we get a vertical plane. Looking back at relationship \eqref{spherical_cartesian}, we see it is only a half plane because $\rho\sin\phi$ cannot be negative.
Constant $\rho$
Most people don't have trouble understanding what $\rho=3$ means. It is the sphere of radius 3 centered at the origin. In general, the surface $\rho=$ constant is a sphere of radius $\rho$ centered at the origin.
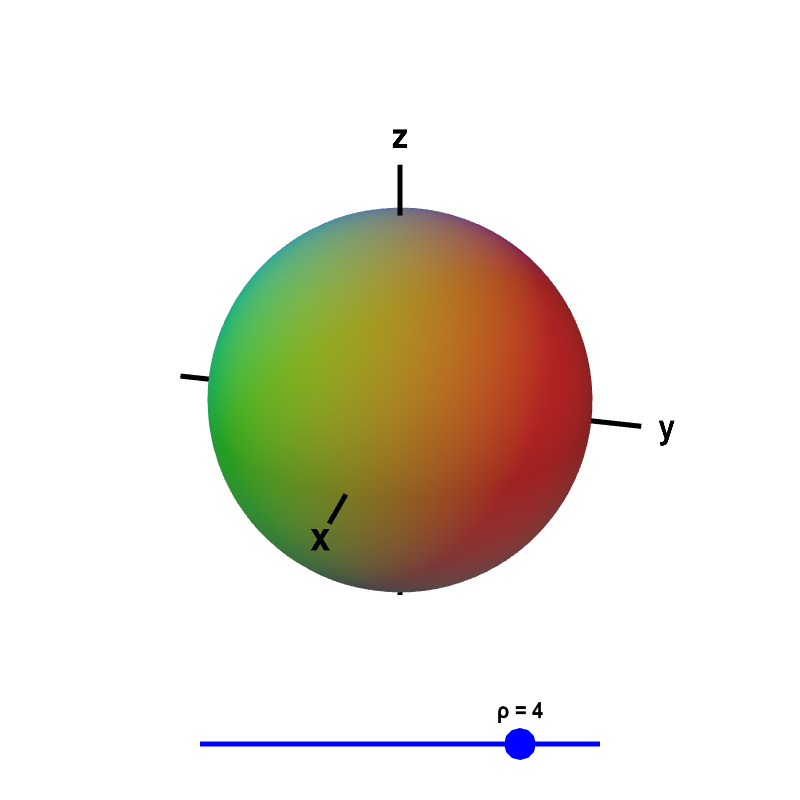
Applet loading
Surfaces of constant $\rho$ in spherical coordinates. The spherical surface of $\rho=$ constant is shown, where the value of $\rho$ is determined by the blue point on the slider.
From relationship \eqref{spherical_cartesian}, we can calculate that \begin{align*} x^2+y^2+z^2 &= \rho^2\sin^2\phi(\cos^2\theta + \sin^2\theta) + \rho^2\cos^2\phi\\ &= \rho^2(\sin^2\phi+\cos^2\phi)\\ &= \rho^2 \end{align*} verifying that $\rho=$ constant is the sphere of radius $\rho$ centered at the origin.
Thread navigation
Vector algebra
- Previous: Surfaces of revolution
- Next: Polar coordinates
Math 2374
Similar pages
- Cartesian coordinates
- Polar coordinates
- Cylindrical coordinates
- Polar coordinates mapping
- Parametrization of a line
- Parametrization of a line examples
- Triple integral change of variable examples
- Lines (and other items in Analytic Geometry)
- The elliptic paraboloid
- The hyperbolic paraboloid
- More similar pages