Math Insight

The hyperbolic paraboloid

With just the flip of a sign, say $$x^2 + y^2 \quad \text{to} \quad x^2 - y^2,$$ we can change from an elliptic paraboloid to a much more complex surface. Because it's such a neat surface, with a fairly simple equation, we use it over and over in examples.

Hyperbolic paraboloids are often referred to as “saddles,” for fairly obvious reasons. Their official name stems from the fact that their vertical cross sections are parabolas, while the horizontal cross sections are hyperbolas. But even the vertical cross sections are more complicated than with an elliptic paraboloid. Look at the below applet, which shows the surface $z = x^2 - y^2$.

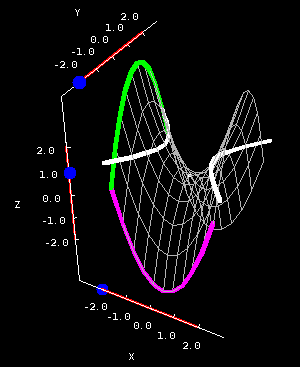
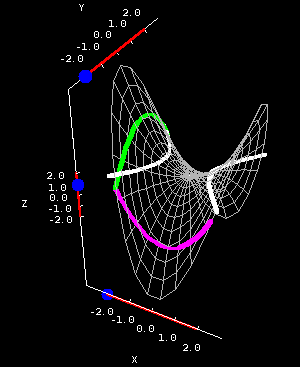
Hyperbolic paraboloid cross sections. The hyperbolic paraboloid $z=x^2-y^2$ is plotted on a square domain $-2 \le x \le 2, -2 \le y \le 2$ in the first panel and on the circular domain $x^2+y^2 \le 8$ in the second panel. You can drag the blue points on the sliders to change the location of the different types of cross sections.

More information about applet.

Notice that the parabolas open in different directions; the green parabolas open downward, while the purple ones open upward. Also, the hyperbolas which make up the horizontal cross sections can open in either the $x$- or $y$- direction, depending on the chosen value for $z$. All of these are important features of any hyperbolic paraboloid.

The second applet lets you explore what happens when you adjust the coefficients of the equation $$z = Ax^2 + By^2.$$ (Here we're assuming $A$ is positive and $B$ is negative; in other words this “looks” like $z = x^2 - y^2$.)

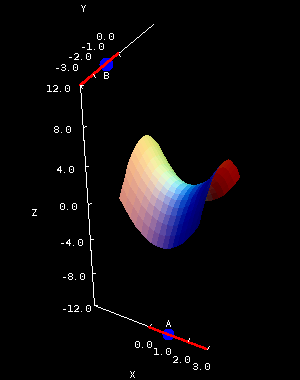
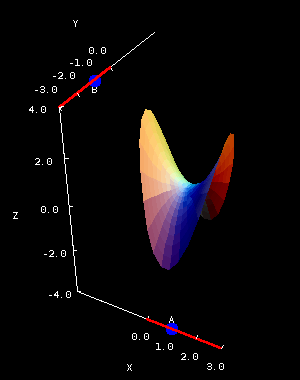
Hyperbolic paraboloid coefficients. The hyperbolic paraboloid $z=Ax^2+By^2$ is plotted on a square domain $-2 \le x \le 2, -2 \le y \le 2$ in the first panel and on the circular domain $x^2+y^2 \le 1.65^2$ in the second panel. You can drag the points to change the coefficients $A$ and $B$. $A$ is constrained to be positive, and $B$ is constrained to be negative.

More information about applet.

Here are a few things for you to think about:

• What does the horizontal cross section given by $z=0$ look like? Check on the first applet, and also look at the equation when $z=0$. Is this still a hyperbola?
• How would $z = y^2 - x^2$ look different than $z = x^2 - y^2$?

Be very careful; if you hear somebody refer simply to a “paraboloid,” they generally mean an elliptic paraboloid, or even a surface where $A=0$ or $B=0$. If you're in doubt which surface somebody means, ask.

The horizontal cross sections of graphs of functions are also called level curves, and you can compare the above horizontal cross sections with how we calculate them as level curves.

List of quadric surfaces

• Elliptic paraboloid
• Hyperbolic paraboloid
• Ellipsoid
• Double cone
• Hyperboloid of one sheet
• Hyperboloid of two sheets