Proper orientation for Stokes' theorem
One important subtlety of Stokes' theorem is orientation. We need to be careful about orientating the surface (which is specified by the normal vector $\vc{n}$) properly with respect to the orientation of the boundary (which is specified by the tangent vector). Remember, changing the orientation of the surface changes the sign of the surface integral. If we choose the wrong $\vc{n}$ (i.e., the wrong orientation), we could be off by a minus sign.
Look at the below applet from the Stokes' theorem introduction, where the “microscopic circulation” is sketched by green circles on the surface. Notice how the arrows on the little green circles (indicating the “microscopic circulation”) are aligned with the red arrow indicating the direction of the curve $\dlc$. If, for example, the arrows on the green circles were going the other direction, the green circles and the red curve wouldn't match, and we'd be off by a minus sign.
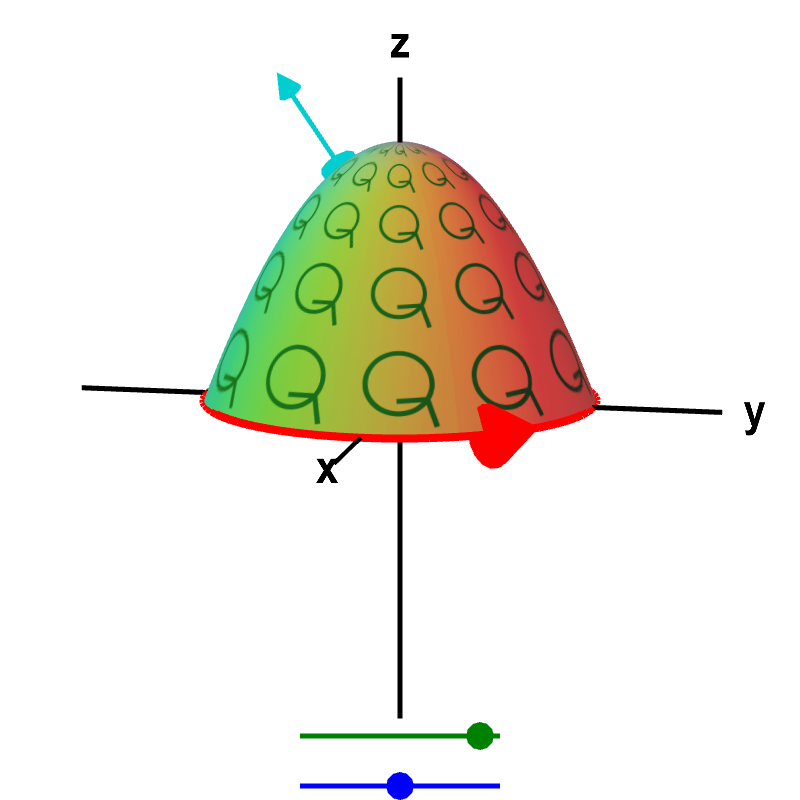
Applet loading
Macroscopic and microscopic circulation in three dimensions. The relationship between the macroscopic circulation of a vector field $\dlvf$ around a curve (red boundary of surface) and the microscopic circulation of $\dlvf$ (illustrated by small green circles) along a surface in three dimensions must hold for any surface whose boundary is the curve. No matter which surface you choose (change by dragging the green point on the top slider), the total microscopic circulation of $\dlvf$ along the surface must equal the circulation of $\dlvf$ around the curve. (We assume that the vector field $\dlvf$ is defined everywhere on the surface.) You can change the curve to a more complicated shape by dragging the blue point on the bottom slider, and the relationship between the macroscopic and total microscopic circulation still holds. The surface is oriented by the shown normal vector (moveable cyan arrow on surface), and the curve is oriented by the red arrow.
Looking from the positive $z$-axis, both the green circles and the red curve indicate counterclockwise circulation. To define the orientation for Green's theorem, this was sufficient. We simply insisted that you orient the curve $\dlc$ in the counterclockwise fashion. For Stokes' theorem, we cannot just say “counterclockwise,” since the orientation that is counterclockwise depends on the direction from which you are looking. If you take the applet and rotate it $180^\circ$ so that you are looking at it from the negative $z$-axis, the same curve would look like it was oriented in the clockwise fashion. Since the green circles would also look like they are oriented in a clockwise fashion, you can still see that the green circles and the red curve match.
Remember, too, that the curve $\dlc$ can be floating or twisted in any direction. It doesn't have to look as simple as in the above examples. Thankfully, choosing the correct orientation doesn't have to be too difficult if you remember the right hand rule. If you look at your right hand from the side of your thumb, your fingers curl in the counterclockwise direction. Think of your thumb as the normal vector $\vc{n}$ of a surface. If your thumb points to the positive side of the surface, your fingers indicate the circulation corresponding to $\curl \dlvf \cdot \vc{n}$. In the above applet, the normal vector corresponding to the orientation of the green circles is shown as a cyan arrow. If you place the thumb of your right hand so that it points in the direction of the cyan normal vector, the fingers of your right hand curl in the direction corresponding to the orientation of the green circles.
With your thumb oriented corresponding to the cyan normal vector, move your hand along the surface toward its edges. When your fingers are next to the boundary of the surface, the red curve $\dlc$ must be oriented (by red arrow) to go around the same direction your fingers are pointing. If the relationship between the normal vector $\vc{n}$ and the orientation of $\dlc$ doesn't match the relationship between the thumb and fingers of your right hand, you'll be off by a minus sign when trying to apply Stokes' theorem.
Another way of thinking about the proper orientation is the following. Imagine that you are walking on the positive side of the surface (i.e, the side with the cyan normal vector in the above applet). If you walk near the edge of the surface in the direction corresponding to the orientation of $\dlc$, then surface must be to your left and the edge $\dlc$ must be to your right.
When the curve $\dlc$ and the surface $\dls$ are oriented as described above so that Stokes' theorem applies, we say that $\dlc$ is a positively oriented boundary of $\dls$.
Thread navigation
Multivariable calculus
- Previous: The idea behind Stokes' theorem
- Next: Stokes' theorem examples
Math 2374
- Previous: The idea behind Stokes' theorem*
- Next: Stokes' theorem examples
Similar pages
- The idea behind Stokes' theorem
- Stokes' theorem examples
- The idea behind Green's theorem
- The definition of curl from line integrals
- Calculating the formula for circulation per unit area
- The integrals of multivariable calculus
- Length, area, and volume factors
- The idea of the curl of a vector field
- Subtleties about curl
- The components of the curl
- More similar pages