Orienting surfaces
Choosing an orientation of a curve is a fairly simply idea. One just needs to choose the direction by which one moves along the curve. However, choosing an orientation of a curve is also equivalent to choosing one of its possible unit tangent vectors.
Orientating a parametrized surfaces is a little trickier than orienting a curve. But, if you think of choosing an orientation as choosing between one of two possible unit vectors, it will help you understand the orientation of surfaces.
Like curves, we can parametrize a surface in two different orientations. The orientation of a curve is given by the unit tangent vector $\vc{n}$; the orientation of a surface is given by the unit normal vector $\vc{n}$. Unless we are dealing with an unusual surface, a surface has two sides. We can pick the normal vector to point out one side of the surface, or we can pick the normal vector to point out the other side of the surface. Our choice of normal vector specifies the orientation of the surface. We call the side of the surface with the normal vector the positive side of the surface.
As an example, consider the sphere of radius $R$ centered at the origin. Using spherical coordinates, we could parametrize the sphere using \begin{align*} \dlsp(\theta,\phi) = (R\sin \phi \cos\theta, R\sin\phi \sin\theta, R\cos\phi) \end{align*} for $0 \le \theta \le 2\pi$ and $0 \le \phi \le \pi$. Remember that a formula for the unit normal vector is \begin{align*} \vc{n} = \frac{\displaystyle \pdiff{\dlsp}{\spfv}(\spfv,\spsv) \times \pdiff{\dlsp}{\spsv}(\spfv,\spsv)}{\displaystyle \left\| \pdiff{\dlsp}{\spfv}(\spfv,\spsv) \times \pdiff{\dlsp}{\spsv}(\spfv,\spsv) \right\|}. \end{align*} only in this case, we have $\theta$ and $\phi$ rather than $\spfv$ and $\spsv$.
Let's find an unit normal vector of the sphere. \begin{align*} \pdiff{\dlsp}{\theta}(\theta,\phi) &= (-R\sin\phi \sin\theta, R\sin\phi \cos\theta,0)\\ \pdiff{\dlsp}{\phi}(\theta,\phi) &= (R\cos\phi \cos\theta, R\cos\phi \sin\theta, -R\sin\phi)\\ \pdiff{\dlsp}{\theta} (\theta,\phi)\times \pdiff{\dlsp}{\phi}(\theta,\phi) &= \left| \begin{array}{ccc} \vc{i} & \vc{j} & \vc{k}\\ -R\sin\phi \sin\theta& R\sin\phi \cos\theta &0\\ R\cos\phi \cos\theta & R\cos\phi \sin\theta & -R\sin\phi \end{array} \right|\\ &= -R^2 \sin^2\phi \cos\theta\, \vc{i} -R^2 \sin^2\phi \sin\theta\, \vc{j}\\ & \quad -R^2 \sin\phi \cos\phi (\sin^2\theta + \cos^2\theta)\vc{k}\\ & = -R^2 \sin^2\phi \cos\theta \,\vc{i} -R^2 \sin^2\phi \sin\theta \, \vc{j}\\ & \quad -R^2 \sin\phi \cos\phi \, \vc{k}\\ & = -R^2\sin\phi \left( \sin\phi \cos\theta \,\vc{i} +\sin\phi \sin\theta \, \vc{j} + \cos\phi \, \vc{k}\right)\\ \left\|\pdiff{\dlsp}{\theta} (\theta,\phi)\times \pdiff{\dlsp}{\phi}(\theta,\phi)\right\| &= R^2\sin \phi \sqrt{\sin^2 \phi \cos^2\theta + \sin^2\phi \sin^2\theta + \cos^2\phi}\\ &= R^2\sin \phi \sqrt{\sin^2\phi( \cos^2\theta + \sin^2\theta) + \cos^2\phi}\\ &= R^2\sin \phi \sqrt{\sin^2\phi + \cos^2\phi}\\ &=R^2\sin \phi \end{align*}
We obtain the unit normal vector \begin{align*} \vc{n} &= \frac{\displaystyle \pdiff{\dlsp}{\theta} (\theta,\phi)\times \pdiff{\dlsp}{\phi}(\theta,\phi)} {\displaystyle \left\|\pdiff{\dlsp}{\theta} (\theta,\phi)\times \pdiff{\dlsp}{\phi}(\theta,\phi)\right\|}\\ &=-\sin\phi \cos\theta \,\vc{i} -\sin\phi \sin\theta \, \vc{j} - \cos\phi \, \vc{k}\\ &=(-\sin\phi \cos\theta, -\sin\phi \sin\theta, - \cos\phi) \end{align*}
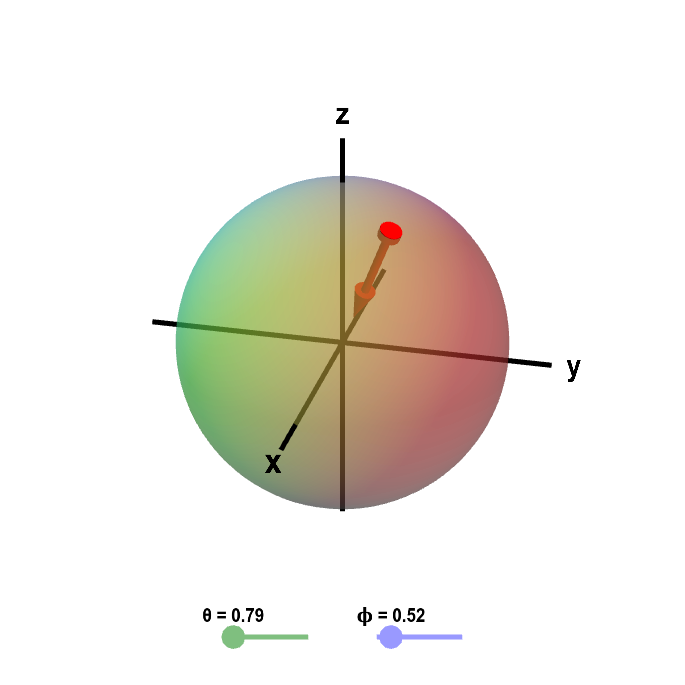
This is the normal vector for the point on the surface given by $$\dlsp(\theta,\phi) = (R\sin \phi \cos\theta, R\sin\phi \sin\theta, R\cos\phi).$$ Note that $\vc{n}$ points in the opposite direction as $\dlsp(\theta,\phi)$ (as $\vc{n}$ is $-1/R$ times $\dlsp(\theta,\phi)$). Consequently, $\vc{n}$ points back toward the origin, i.e., points inside the sphere. For example, if $\theta=0$ and $\phi=\pi/2$, then $\dlsp(0,\pi/2) = (R,0,0)$ and $\vc{n}=(-1,0,0)$. The vector $\vc{n}$ for any value of $\theta$ or $\phi$ is shown in the figure below. Notice that $\vc{n}$ always points toward the inside of the sphere. In this case, the inside of the sphere is the positive side of the surface.
Applet loading
Sphere with inward normal vector. The sphere of a fixed radius $R$ is parametrized by $\dlsp(\theta,\phi) = (R\sin \phi \cos\theta, R\sin\phi \sin\theta, R\cos\phi)$ for $0 \le \theta \le 2\pi$ and $0 \le \phi \le \pi$. In this case, we have chosen the inward pointing normal vector $\vc{n} = (-\sin \phi \cos\theta, -\sin\phi \sin\theta, -\cos\phi),$ orienting the surface so the inside is the positive side. You can change the values of $\theta$ and $\phi$ by moving the base of the normal vector or by dragging the points on the sliders.
We could also orient the surface by choosing the normal vector $\pdiff{\dlsp}{\phi} \times \pdiff{\dlsp}{\theta}$ instead of the vector $\pdiff{\dlsp}{\theta} \times \pdiff{\dlsp}{\phi}$ that we used above. How does the new normal vector orient the surface?
Recalling the properties
of the cross product,
we can conclude these vectors are opposites: $\displaystyle
\pdiff{\dlsp}{\phi} \times \pdiff{\dlsp}{\theta} = -\pdiff{\dlsp}{\theta} \times
\pdiff{\dlsp}{\phi}$. In this case, unit normal is
\begin{align*}
\vc{n} = \frac{\displaystyle\pdiff{\dlsp}{\phi} \times \pdiff{\dlsp}{\theta}}
{\displaystyle\left\| \pdiff{\dlsp}{\phi} \times \pdiff{\dlsp}{\theta} \right\|}
= (\sin\phi \cos\theta, \sin\phi \sin\theta,\cos\phi)
\end{align*}
The normal vector points toward the outside the sphere, as shown below. For this second
orientation of the sphere, the outside is the positive side of the
surface.
Sphere with outward normal vector. The sphere of a fixed radius $R$ is parametrized by
$\dlsp(\theta,\phi) = (R\sin \phi \cos\theta, R\sin\phi \sin\theta, R\cos\phi)$
for $0 \le \theta \le 2\pi$ and $0 \le \phi \le \pi$. In this case, we have chosen the outward pointing normal vector
$\vc{n} = (\sin \phi \cos\theta, \sin\phi \sin\theta, \cos\phi),$
orienting the surface so the outside is the positive side. You can change the values of $\theta$ and $\phi$ by moving the base of the normal vector or by dragging the points on the sliders.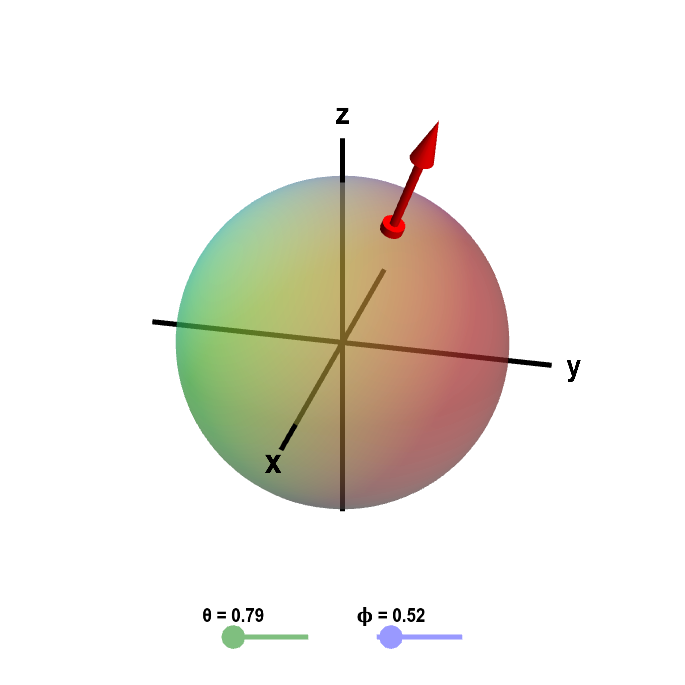
Applet loading
Thread navigation
Multivariable calculus
Math 2374
Notation systems
Similar pages
- A Möbius strip is not orientable
- An introduction to parametrized surfaces
- Surface area of parametrized surfaces
- Normal vector of parametrized surfaces
- Parametrized surface examples
- Calculation of the surface area of a parametrized surface
- Parametrized surface area example
- Parametrization of a line
- Parametrization of a line examples
- An introduction to parametrized curves
- More similar pages