The definition of curl from line integrals
We can get a pretty good intuition behind the formula for the components of the curl by just visualizing spinning spheres immersed in fluid. However, to really master curl and the meaning of its components, you need to understand the basis of curl from the circulation that is captured by line integrals.
In fact, the way one formally defines the curl of a vector field is through line integrals. We define the vector $\curl \dlvf$ by prescribing an expression for any component $\curl \dlvf \cdot \vc{u}$ of the curl vector in the direction of the unit vector $\vc{u}$. To define the curl at a point $\vc{a} \in \R^3$, we let $\dlc$ be a closed curve around $\vc{a}$ lying in a plane perpendicular to $\vc{u}$. We orient $\dlc$ by the right-hand rule, so that when the fingers of your right hand curl in the direction of the orientation of $\dlc$, your right thumb points in the direction of $\vc{u}$.
The circulation of the vector field $\dlvf: \R^3 \to \R^3$ (confused?) around $\dlc$ is given by the line integral of $\dlvf$ around $\dlc$: $\dlint.$ The line integral is just a number, and if we divide it by the area inside $\dlc$, which we'll denote by $A(\dlc)$, we get an expression for the circulation per unit area: $$\frac{1}{A(\dlc)} \dlint.$$
We define the component $\curl \dlvf(\vc{a}) \cdot \vc{u}$ of the curl of $\dlvf$ at point $\vc{a}$ in the direction $\vc{u}$ as the limit of this circulation per unit area as the curve $\dlc$ shrinks to a point, i.e., as the area $A(\dlc)$ goes to zero: \begin{align*} \curl \dlvf(\vc{a}) \cdot \vc{u} = \lim_{A(\dlc)\to 0} \frac{1}{A(\dlc)} \dlint. \end{align*}
To make sure this definition is valid, one would need to show that this limit converges to a number and that this number doesn't depend on the choice of $\dlc$. But we won't address those details here. Let's just assume this definition works out.
We can use this definition to set up line integrals that should give the formulas for the curl components in the directions of the standard unit vectors. Let's focus on the $z$ component $\curl \dlvf \cdot \vc{k}$. We can visualize this component as the rotation of a ball on a rod parallel to the $z$-axis.
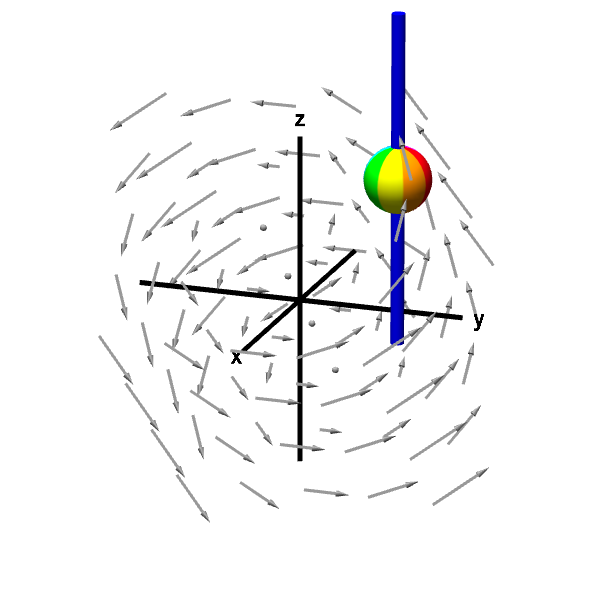
Applet loading
A rotating sphere on a rod gives z-component of curl. The rod constrains the rotation of the sphere to point (using the right hand rule) in either the positive or negative $z$ direction. The speed of this rotation corresponds to the $z$-component of the curl.
According to our above definition, we need to construct a curve centered at the sphere's location in a plane parallel to the $xy$-plane. The curve must be oriented with the right-hand rule to correspond to $\vc{k}$, or the positive $z$ direction, i.e., it should be oriented counterclockwise when viewed from the positive $z$-axis. The following applet illustrates such a curve.
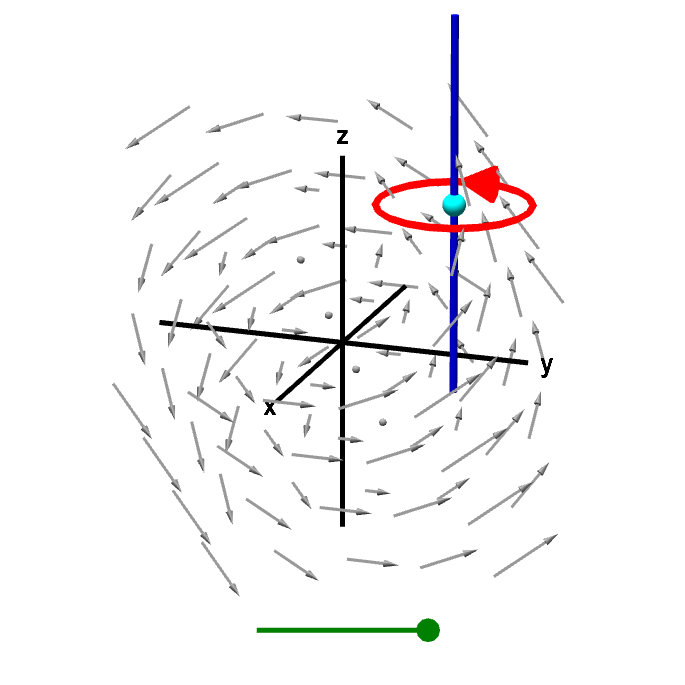
Applet loading
A line integral gives z-component of curl. A line integral around a curve in a plane perpendicular to the $z$-axis gives circulation of the vector field corresponding to the $z$-component of the curl. Dividing this line integral the the area of the region inside the curve, and letting the curve shrink to zero gives circulation per unit area. This circulation per unit area is the $z$-component of the curl. You can drag the green point on the slider to shrink the curve to a point or drag the cyan point to change the location where the $z$-component of the curl is being calculated.
The integral $\dlint$ measures the circulation around $\dlc$. To estimate the “microscopic circulation,” corresponding to $\curl \dlvf \cdot \vc{k}$, we just need to divide by the area inside $\dlc$ and let $\dlc$ shrink to a point. By comparing the above two applets, you can see how the circulation of $\dlvf$ around $\dlc$ captures the “microscopic circulation,” that would make a tiny sphere on the rod spin.
To obtain a formula for $\curl \dlvf \cdot \vc{k}$, we need to choose a particular $\dlc$. The simplest case is to make $\dlc$ be a rectangle. You can read a sketch of the proof why for such a $\dlc$, we obtain that the $z$-component of the curl is \begin{align*} \curl \dlvf \cdot \vc{k} = \pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y}. \end{align*}
One can perform similar calculations to determine the formulas for the other components of the curl, as given in the page introducing the curl components.
Thread navigation
Multivariable calculus
Math 2374
Notation systems
Similar pages
- The idea behind Green's theorem
- Calculating the formula for circulation per unit area
- The idea behind Stokes' theorem
- The idea of the curl of a vector field
- Subtleties about curl
- The components of the curl
- Line integrals as circulation
- A path-dependent vector field with zero curl
- Proper orientation for Stokes' theorem
- Stokes' theorem examples
- More similar pages