Math Insight

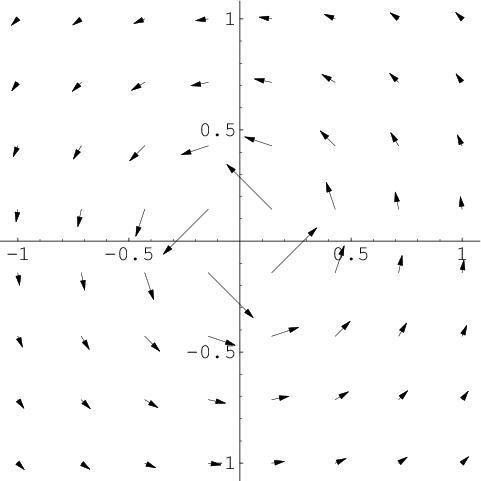
A path-dependent vector field with zero curl

Our goal is to determine if the vector field

$$\begin{align*} \dlvf(x,y) = \left( \frac{-y}{x^2+y^2}, \frac{x}{x^2+y^2} \right) \end{align*}$$ is conservative (also called path-independent).

One condition for path independence is the following. For a simply connected domain, a continuously differentiable vector field $\dlvf$ is path-independent if and only if its curl is zero.

Since $\dlvf(x,y)$ is two dimensional, we need to check the scalar curl

$$\begin{align*} \pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y}. \end{align*}$$ We calculate $$\begin{align*} \pdiff{\dlvfc_2}{x} &= \frac{1}{x^2+y^2} - \frac{x(2x)}{(x^2+y^2)^2} = \frac{y^2-x^2}{(x^2+y^2)^2}\\ \pdiff{\dlvfc_1}{y} &= -\frac{1}{x^2+y^2} +\frac{y(2y)}{(x^2+y^2)^2} = \frac{y^2-x^2}{(x^2+y^2)^2}. \end{align*}$$ Since these partial derivatives are equal, the curl is zero.

Can we conclude $\dlvf$ is conservative? The problem is that $\dlvf$ is not defined at the origin $(0,0)$. Its domain of definition has a hole in it, which for two-dimensional regions, is enough to prevent it from being simply connected. The test does not apply, and we still don't know whether or not $\dlvf$ is conservative.

Let's try another test, this time a test for path-dependence. If we can find a closed curve along which the integral of $\dlvf$ is nonzero, then we can conclude that $\dlvf$ is path-dependent. If the curve does not go around the origin, then we can use Green's theorem to show the integral of $\dlvf$ zero,

$$\begin{align*} \lint{\adlc}{\dlvf}= \int_\dlr \left(\pdiff{\dlvfc_2}{x}-\pdiff{\dlvfc_1}{y}\right) dA = \int_\dlr 0 dA = 0, \end{align*}$$ as the vector field is defined everywhere in the region $\dlr$ inside the closed curve $\adlc$.

We must try a closed curve where Green's theorem does not apply, i.e., one that goes around the point at the origin where $\dlvf$ is not defined. We'll use the unit circle.

A counterclockwise parametrization of the unit circle is $\dllp(t)=(\cos t, \sin t)$ for $0 \le t \le 2\pi$. On the unit circle, $\dlvf$ takes a simple form,

$$\begin{align*} \dlvf(\dllp(t)) &= \dlvf(\cos t, \sin t) = \left(\frac{-\sin t}{\cos^2 t + \sin^2 t}, \frac{\cos t}{\cos^2 t+ \sin^2 t}\right)\\ &= (-\sin t, \cos t). \end{align*}$$ Therefore, $$\begin{align*} \dlint &= \dplint\\ &= \int_0^{2\pi} (-\sin t, \cos t) \cdot (-\sin t, \cos t) dt\\ &= \int_0^{2\pi} (\sin^2 t + \cos^2 t) dt = \int_0^{2\pi} 1\, dt = 2\pi. \end{align*}$$

The hole in the domain at the origin did end up causing trouble. We found a curve $\dlc$ where the circulation around $\dlc$ is not zero. The vector field $\dlvf$ is path-dependent.

This vector field is the two-dimensional analogue of one we used to illustrate the subtleties of curl, as it had curl-free macroscopic circulation. The circulation can be clearly seen by plotting the vector field $\dlvf$. It's difficult to plot, because the vector field blows up at the origin.

Further insight into $\dlvf$ can be obtained from the fact that $\dlvf$ has a potential function if, for example, you restrict yourself to the right half-plane with $x>0$. In this case, you can write $\dlvf(x,y) = \nabla f(x,y)$, where $f(x,y) = \arctan(y/x)$. Of course, this potential function cannot be extended to the whole plane, or we'd run into a contradiction with the fact that $\dlint \ne 0$ when $\dlc$ is the unit circle. Besides not being defined along the line $x=0$, it is also discontinuous across that line. But, the existence of this potential function explains why the curl should be zero away from the line $x=0$. (The whole line $x=0$ isn't special for $\dlvf$, as the origin is the only point that causes problems. You could, for example, use $f(x,y) = -\arctan(x/y)$ for a potential function away from the line $y=0$.)

Thread navigation

Multivariable calculus

• Previous: A conservative vector field has no circulation
• Next: Testing if three-dimensional vector fields are conservative

Math 2374

• Previous: A conservative vector field has no circulation
• Next: Testing if three-dimensional vector fields are conservative

Notation systems

Select a notation system:
default Marsden and Tromba Stewart

More information on notation systems

Similar pages

• A conservative vector field has no circulation
• Subtleties about curl
• The idea behind Green's theorem
• Calculating the formula for circulation per unit area
• The gradient theorem for line integrals
• How to determine if a vector field is conservative
• Finding a potential function for conservative vector fields
• Finding a potential function for three-dimensional conservative vector fields
• A simple example of using the gradient theorem
• Testing if three-dimensional vector fields are conservative
• More similar pages