Introduction to a line integral of a vector field
A line integral (sometimes called a path integral) is the integral of some function along a curve. One can integrate a scalar-valued function along a curve, obtaining for example, the mass of a wire from its density. One can also integrate a certain type of vector-valued functions along a curve. These vector-valued functions are the ones where the input and output dimensions are the same, and we usually represent them as vector fields.
One interpretation of the line integral of a vector field is the amount of work that a force field does on a particle as it moves along a curve. To illustrate this concept, we return to the slinky example we used to introduce arc length. Here, our slinky will be the helix parameterized by the function $\dllp(t) = (\cos t, \sin t, t/(3\pi))$, for $0 \le t \le 6\pi$,
Imagine that you put a small magnetized bead on your slinky (the bead has a small hole in it, so it can slide along the slinky). Next, imagine that you put a large magnet to the left of the slink, as shown by the large green square in the below applet. The magnet will induce a magnetic field $\dlvf(x,y,z)$, shown by the green arrows.
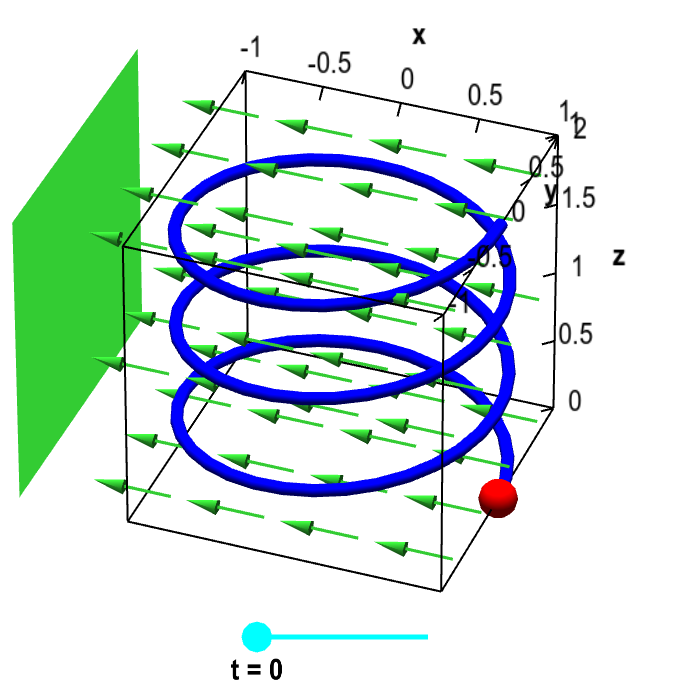
Applet loading
Particle on helix with magnet. The blue helix is parametrized by $\dllp(t) = (\cos t, \sin t, t/(3\pi))$, for $0 \le t \le 6\pi$. For a given value of $t$ (changed by the cyan point on the slider), the red point represents a magnetic bead at point $\dllp(t)$. The green rectangle represents a large magnet, which induces the constant magnetic field represented by the vector field $\dlvf(x,y,z) = (-1/2, 0, 0)$ and illustrated with the green arrows. The magnetic field does work on the bead as it moves along the curve.
Since the bead is magnetized, the magnetic field exerts a force on the bead. However, we'll assume the bead's position is constrained be at $\dllp(t)$. We'll ignore any effects of the magnetic force on the position of the bead.
As you change $t$ to move the bead, work is done by the magnetic field on the bead. Work equals forces times distance. If the magnetic field were aligned with the direction of movement, calculating the work would be simple.
However, the bead does not move in the direction of the magnetic field. It is constrained to move along the slinky. The work is calculated from the component of the force in the direction of movement. For example, when the movement is 90 degrees from the direction of the force, the magnetic field does no work.
First, what is the direction of movement? It is the direction given by the velocity $\dllp'(t)$. Denote by $\vc{T}$ the unit vector in the direction of movement: $\vc{T}(t) = \dllp'(t)/\|\dllp'(t)\|$. Since $\dllp'(t)$ (and therefore $\vc{T}$) is tangent to the path, we refer to $\vc{T}$ as the unit tangent vector. It is shown by the blue vector in the below figure.
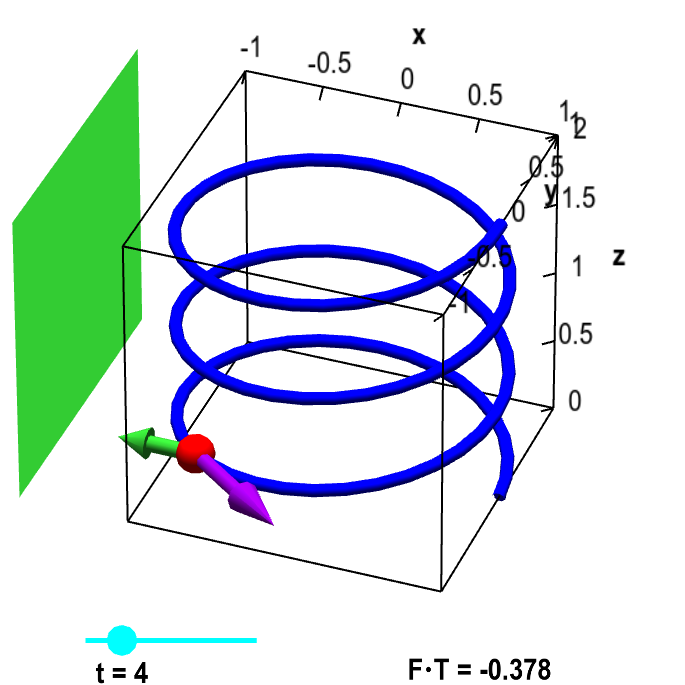
Applet loading
Particle on helix with magnet and tangent vector. The blue helix is parametrized by $\dllp(t) = (\cos t, \sin t, t/(3\pi))$, for $0 \le t \le 6\pi$. For a given value of $t$ (changed by the cyan point on the slider), the red point represents a magnetic bead at point $\dllp(t)$. The purple vector represents the tangent vector $\vc{T}$ in the direction of the particle's movement for increasing $t$. The green rectangle represents a large magnet, which induces the constant magnetic field represented by the vector field $\dlvf(x,y,z) = (-1/2, 0, 0)$ and illustrated with the green vector. The work done by the magnetic field on the particle is determined by the component $\dlvf \cdot \vc{T}$ of the magnetic field vector $\dlvf$ in the direction of the tangent vector $\vc{T}$, the value of which is shown in the lower right corner.
The component of the force in the direction of movement is simply the dot product of the force $\dlvf$ at the point $\dllp(t)$ with the tangent vector $\vc{T}(t)$, i.e., it is $\dlvf(\dllp(t)) \cdot \vc{T}(t)$. For shorthand, we'll write it as $\dlvf \cdot \vc{T}$. This number is displayed by the cyan mark on the green slider. Recall that the dot product is zero if the two vectors are orthogonal, is negative if their angle is greater than 90 degrees, and is positive if their angle is less than 90 degrees.
If we multiply the (component of) force $\dlvf \cdot \vc{T}$ by distance, we get work. Consequently, we can think of $\dlvf \cdot \vc{T}$ as a scalar-valued function that gives work per unit length along the slinky. To get the total work, we simply need to take the line integral of this scalar-valued function. In other words, the total work is \begin{align*} \text{Work} = \slint{\dlc}{\dlvf \cdot \vc{T}}, \end{align*} where $\dlc$ is the path of the slinky. This integral adds up the product of force ($\dlvf \cdot \vc{T}$) and distance ($d\als$) along the slinky, which is work.
To derive a formula for this work, we use the formula for the line integral of a scalar-valued function $\dlsi$ in terms of the parameterization $\dllp(t)$, \begin{align*} \slint{\dlc}{\dlsi}=\dpslint \end{align*} When we replace $\dlsi$ with $\dlvf \cdot \vc{T}$, we get \begin{align*} \slint{\dlc}{\dlvf \cdot \vc{T}} = \int_a^b \dlvf(\dllp(t)) \cdot \vc{T}(t)\| \dllp'(t) \| dt, \end{align*} where for our parametrization $\dllp(t)$ of the slinky, $a=0$ and $b=6\pi$.
We can simplify this further. Remember that $\vc{T}(t) = \dllp'(t)/\|\dllp'(t)\|$. Consquently, the two occurrences of $\|\dllp'(t)\|$ cancel, and we are left with \begin{align*} \slint{\dlc}{\dlvf \cdot \vc{T}} = \dplint. \end{align*} We usually write $\vc{T} \, d\als$ as $d\lis$. Hence, the important formula to know is that the line integral of a vector field is \begin{align*} \dlint = \dplint, \end{align*} where the curve $\dlc$ is parametrized by the function $\dllp(t)$ for $a \le t \le b$.
The fundamental role of line integrals in vector calculus
The line integral of a vector field plays a crucial role in vector calculus. Out of the four fundamental theorems of vector calculus, three of them involve line integrals of vector fields. Green's theorem and Stokes' theorem relate line integrals around closed curves to double integrals or surface integrals. If you have a conservative vector field, you can relate the line integral over a curve to quantities just at the curve's two boundary points. It's worth the effort to develop a good understanding of line integrals.
Thread navigation
Multivariable calculus
- Previous: Introduction to a line integral of a scalar-valued function
- Next: Line integrals are independent of parametrization
Math 2374
Notation systems
Similar pages
- Introduction to a line integral of a scalar-valued function
- Line integrals are independent of parametrization
- Examples of scalar line integrals
- Alternate notation for vector line integrals
- Line integrals as circulation
- Vector line integral examples
- The arc length of a parametrized curve
- The idea behind Green's theorem
- The integrals of multivariable calculus
- Length of curves
- More similar pages