The idea of the divergence of a vector field
Both the divergence and curl are vector operators whose properties are revealed by viewing a vector field as the flow of a fluid or gas. Here we focus on the geometric properties of the divergence; you can read a similar discussion of the curl on another page.
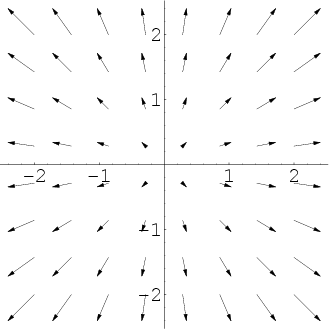
The divergence of a vector field is relatively easy to understand intuitively. Imagine that the vector field $\dlvf$ pictured below gives the velocity of some fluid flow. It appears that the fluid is exploding outward from the origin.
This expansion of fluid flowing with velocity field $\dlvf$ is captured by the divergence of $\dlvf$, which we denote $\div \dlvf$. The divergence of the above vector field is positive since the flow is expanding.
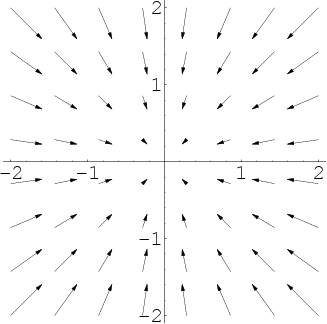
In contrast, the below vector field represents fluid flowing so that it compresses as it moves toward the origin. Since this compression of fluid is the opposite of expansion, the divergence of this vector field is negative.
The divergence is defined for both two-dimensional vector fields $\dlvf(x,y)$ and three-dimensional vector fields $\dlvf(x,y,z)$. A three-dimensional vector field $\dlvf$ showing expansion of fluid flow is shown in the below applet. Again, because of the expansion, we can conclude that $\div \dlvf(x,y)>0$.

Applet loading
Divergent vector field. Three-dimensional vector field used to illustrate fluid flow with positive divergence. You can rotate the graph with the mouse to view from different angles.
Now, imagine that one placed a sphere $\dls$ in the fluid flow centered at the origin. It is clear that the fluid is flowing out of the sphere.
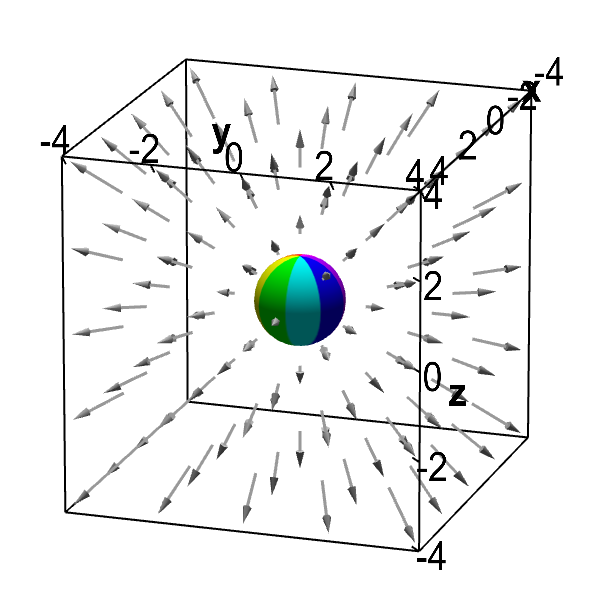
Applet loading
Divergent vector field with embedded sphere. A sphere is embedded in an expanding vector field that could represent fluid flow. The fact that fluid is flowing out of the sphere is a sign of the positive divergence of the vector field. Rotate with mouse to change perspective.
You can move the sphere by dragging it with the mouse. No matter the sphere's position, more fluid is flowing out of the sphere than into the sphere. This fact suggests that the vector field has positive divergence everywhere.
When you learn about the divergence theorem, you will discover that the divergence of a vector field and the flow out of spheres are closely related. For a basic understanding of divergence, it's enough to see that if a fluid is expanding (i.e., the flow has positive divergence everywhere inside the sphere), the net flow out of a sphere will be positive.
Since the above vector field has positive divergence everywhere, the flow out of the sphere will be positive even if we move the sphere away from the origin. Can you see why flow out is still positive even when you move the sphere around with the mouse?
Notice that the arrows continue to get longer as one moves away from the origin so that the fluid is flowing faster when it exits the sphere than when it enters. Moreover, since the arrows are radiating outward, the fluid is always entering the sphere over less than half its surface and is exiting the sphere over greater than half its surface. Hence, the flow out of the sphere is always greater than the flow into the sphere.
The divergence of a vector field simply measures how much the flow is expanding at a given point. It does not indicate in which direction the expansion is occuring. Hence (in contrast to the curl of a vector field), the divergence is a scalar. Once you know the formula for the divergence, it's quite simple to calculate the divergence of a vector, such as in this example.
Observing divergence from pictures?
Warning: these simple examples of visualizing divergence might be misleading. Estimating divergence from a picture is not so simple as it might seem from the above discussion, which was intentionally oversimplified to illustrate the concept of divergence. Detecting expansion of a fluid flow is not simply a matter of looking for flow that is radiating outward. In fact, one could have flow that radiates outward even as a fluid is compressing (which could occur if the flow is slowing down as it moves outward). To protect yourself from being mislead by pictures of vector fields, check out some examples illustrating subtleties of the divergence.
Thread navigation
Multivariable calculus
- Previous: Vector fields as fluid flow
- Next: Subtleties about divergence
Math 2374
- Previous: Vector fields as fluid flow
- Next: The idea of curl of a vector field*