Calculating the formula for circulation per unit area
Given the definition for a component of the curl in the direction of a unit vector, we can sketch a proof for the formula of the “microscopic circulation” that we identify with curl. For simplicitiy, we will focus on the $z$-component of the curl, $\curl \dlvf \cdot \vc{k}$, which is defined as \begin{align*} \curl \dlvf(\vc{a}) \cdot \vc{k} = \lim_{A(\dlc)\to 0} \frac{1}{A(\dlc)} \dlint, \end{align*} for a curve $\dlc$ around the point $\vc{a}=(a,b,c)$ in a plane that is parallel to the $xy$-plane. In the above limit, we let $\dlc$ shrink to a point so that the area $A(\dlc)$ inside $\dlc$ reduces to zero, as illustrated in the below applet. Since we divided by the area $A(\dlc)$, we can interpret curl as being a “circulation per unit area.”
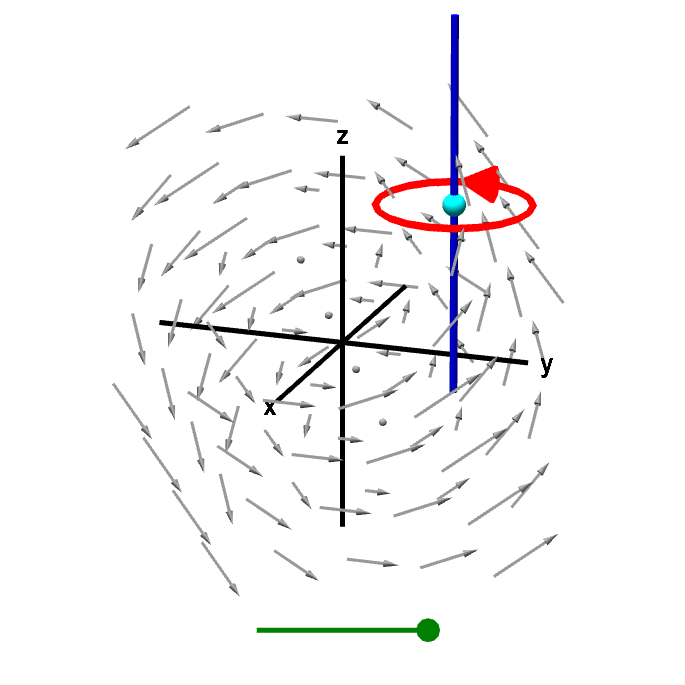
Applet loading
A line integral gives z-component of curl. A line integral around a curve in a plane perpendicular to the $z$-axis gives circulation of the vector field corresponding to the $z$-component of the curl. Dividing this line integral the the area of the region inside the curve, and letting the curve shrink to zero gives circulation per unit area. This circulation per unit area is the $z$-component of the curl. You can drag the green point on the slider to shrink the curve to a point or drag the cyan point to change the location where the $z$-component of the curl is being calculated.
The curve $\dlc$ is contained in the plane parallel to the $xy$-plane that passes through $\vc{a}$, i..e., the plane given by $z=c$. In the integral, we can eliminate $z$ by replacing it with the constant value $c$. Moreover, the tangent vectors along $\dlc$ must be parallel to the $xy$ plane, which means their $z$-components will be zero. Since the line integral of a vector field integrates the tangent components of the vector field, the $z$-component of $\dlvf$ will drop out of the integral $\dlint$. Hence, we can, without loss of generality, replace our three-dimensional vector field $\dlvf(x,y,z)$ with a two-dimensional vector field $\dlvf(x,y)$ consisting of the first two components of the original $\dlvf$ evaluated at $z=c$. We can then view the curve $\dlc$ as lying in the $xy$-plane.
Besides simplifying the notation, this change of perspective make explicit the fact that this calculation is also valid for calculating the “microscopic circulation” of two-dimensional vector fields, like we need for Green's theorem. We just need to remember that, by the right hand rule, positive values of the circulation correspond to counterclockwise rotation in the $xy$-plane.
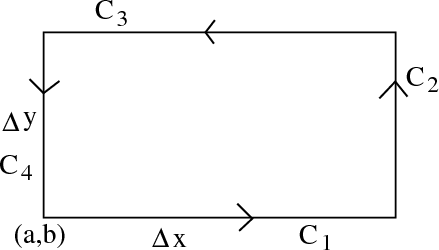
The introductory pages give some intuition why the “circulation per unit area” of the $z$-component of the curl is \begin{align*} \curl \dlvf \cdot \vc{k} = \pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y}. \end{align*} Here we sketch a proof why \begin{align*} \frac{1}{A(\dlc)} \dlint \to \pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y} \end{align*} as we let $\dlc$ shrink to a point. Rather than use the circular $\dlc$ illustrated in the above applet, we let $\dlc$ be a rectangular curve, oriented counterclockwise. For simplicity of the notation, we'll let $(a,b)$ be the lower-left point of $\dlc$ rather than being in the middle. Let the width and height of $\dlc$ be $\Delta x$ and $\Delta y$, respectively. Label the edges of the rectangle by $\dlc_1$, $\dlc_2$, $\dlc_3$, and $\dlc_4$.
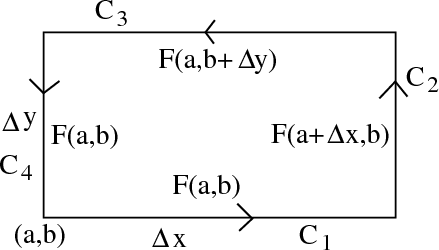
We assume the rectangle is small enough to approximate $\dlvf$ as constant along each edge. Along the curve $\dlc_1$, the value of $y$ is constantly $b$, but the value of $x$ changes from $a$ to $a + \Delta x$. We assume we can ignore that change in $x$ (since the rectangle is small), and simply approximate $\dlvf(x,y)$ as $\dlvf(a,b)$ all along the segment $\dlc_1$.
Along the curve $\dlc_2$, the value of $x$ is constantly $a+\Delta x$, but $y$ changes from $b$ to $b + \Delta y$. Since we assume we can ignore the change in $y$, we approximate $\dlvf(x,y)$ as $\dlvf(a + \Delta x, b)$ all along segment $\dlc_2$.
Similiarly, we approximate $\dlvf(x,y)$ as $\dlvf(a, b + \Delta y)$ all along segment $\dlc_3$ and approximate $\dlvf(x,y)$ as $\dlvf(a,b)$ all along segment $\dlc_4$. We summarize these approximations in the following figure.
Next, to compute the integral $\dlint$, we remember that it is the same thing as integrating the scalar-valued function $\dlvf\cdot \vc{T}$, where $\vc{T}$ is the unit tangent vector along $\dlc$: \begin{align*} \dlint = \slint{\dlc}{\dlvf \cdot \vc{T}}. \end{align*}
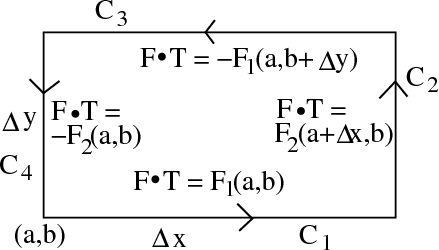
We need to compute $\dlvf \cdot \vc{T}$ along each segment of $\dlc$. The tangent vector $\vc{T}$ is constant along each segment, and we are approximating $\dlvf$ as constant along each segment, so the dot product $\dlvf \cdot \vc{T}$ will be constant along each segment of $\dlc$.
Along $\dlc_1$, the path is directed in the positive $x$ direction, so the unit tangent vector is $\vc{T}=(1,0)$. The dot product $\dlvf \cdot \vc{T}$ is simply the first component of $\dlvf(a,b)$: \begin{align*} \dlvf \cdot \vc{T} = \dlvfc_1(a,b). \end{align*}
Along $\dlc_2$, the path is directed in the positive $y$ direction, so $\vc{T}=(0,1)$, and $\dlvf \cdot \vc{T}$ is simply the second component of $\dlvf(a+\Delta x,b)$: \begin{align*} \dlvf \cdot \vc{T} = \dlvfc_2(a+\Delta x,b). \end{align*}
Along $\dlc_3$, the path is directed in the negative $x$ direction, so the unit tangent vector is $\vc{T}=(-1,0)$. The dot product $\dlvf \cdot \vc{T}$ is minus the first component of $\dlvf(a,b+\Delta y)$: \begin{align*} \dlvf \cdot \vc{T} = -\dlvfc_1(a,b+\Delta y). \end{align*}
Along $\dlc_4$, the path is directed in the negative $y$ direction, so $\vc{T}=(0,-1)$, and $\dlvf \cdot \vc{T}$ is minus the second component of $\dlvf(a,b)$: \begin{align*} \dlvf \cdot \vc{T} = -\dlvfc_2(a,b). \end{align*}
We summarize these findings in the following figure.
The integrals are now easy to compute. Along $\dlc_1$, $\dlvf \cdot \vc{T}$ is constant, so the integral is simply its value $\dlvfc_1(a,b)$ times the length of the segment $\Delta x$: \begin{align*} \lint{\dlc_1}{\dlvf} = \slint{\dlc_1}{\dlvf \cdot \vc{T}} = \slint{\dlc_1}{\dlvfc_1(a,b)} = \dlvfc_1(a,b)\Delta x. \end{align*} Along $\dlc_2$, the integral is $\dlvfc_2(a+\Delta x,b)$ times its length $\Delta y$: \begin{align*} \lint{\dlc_2}{\dlvf} = \dlvfc_2(a+\Delta x,b)\Delta y. \end{align*} Similarly, \begin{align*} \lint{\dlc_3}{\dlvf} = -\dlvfc_1(a,b+\Delta y) \Delta x, \end{align*} and \begin{align*} \lint{\dlc_4}{\dlvf} = -\dlvfc_2(a,b)\Delta y. \end{align*}
The integral around all of $\dlc$ is just the sum along the four segments \begin{align*} \dlint &= \lint{\dlc_1}{\dlvf} +\lint{\dlc_2}{\dlvf} +\lint{\dlc_3}{\dlvf} +\lint{\dlc_4}{\dlvf}\\ &= \dlvfc_1(a,b) \Delta x + \dlvfc_2(a+\Delta x,b) \Delta y - \dlvfc_1(a,b+\Delta y)\Delta x - \dlvfc_2(a,b) \Delta y. \end{align*}
The circulation per unit area is the integral divided by the area of the rectangle, which is $\Delta x \Delta y$ \begin{align*} \frac{\dlint}{\Delta x \Delta y} =\frac{\dlvfc_2(a+\Delta x,b) \Delta y - \dlvfc_2(a,b) \Delta y - (\dlvfc_1(a,b+\Delta y)\Delta x - \dlvfc_1(a,b) \Delta x)}{\Delta x \Delta y}. \end{align*}
Half of the numerator is multiplied by $\Delta y$ and half is multiplied by$\Delta x$. If we separate these into two fractions, we can cancel the $\Delta y$ in the first fraction with the $\Delta y$ in the demoninator \begin{align*} \frac{\dlvfc_2(a+\Delta x,b) \Delta y - \dlvfc_2(a,b) \Delta y}{\Delta x \Delta y} = \frac{\dlvfc_2(a+\Delta x,b) -\dlvfc_2(a,b)}{\Delta x}. \end{align*}
In the second fraction, we can cancel the $\Delta x$, \begin{align*} \frac{\dlvfc_1(a,b+\Delta y)\Delta x - \dlvfc_1(a,b) \Delta x}{\Delta x \Delta y} = \frac{\dlvfc_1(a,b+\Delta y) - \dlvfc_1(a,b)}{\Delta y}. \end{align*} Putting these back together, we have \begin{align*} \frac{\dlint}{\Delta x \Delta y}= \frac{ \dlvfc_2(a+\Delta x,b) - \dlvfc_2(a,b)}{\Delta x} - \frac{\dlvfc_1(a,b+\Delta y) -\dlvfc_1(a,b)}{\Delta y}. \end{align*}
Now, we let the curve $\dlc$ shrink down to a point. This means that $\Delta x \to 0$ and $\Delta y \to 0$. In this limit, the two fractions become something familar: partial derivatives of $\dlvf$. \begin{align*} \lim_{\Delta x, \Delta y \to 0} \frac{\dlint}{\Delta x \Delta y} &= \lim_{\Delta x \to 0} \frac{ \dlvfc_2(a+\Delta x,b) - \dlvfc_2(a,b)}{\Delta x} - \lim_{\Delta y \to 0} \frac{\dlvfc_1(a,b+\Delta y) -\dlvfc_1(a,b)}{\Delta y}\\ &= \pdiff{\dlvfc_2}{x}(a,b) - \pdiff{\dlvfc_1}{y}(a,b). \end{align*}
Therefore, the circulation per unit area around the point $(x,y)=(a,b)$ is \begin{align*} \pdiff{\dlvfc_2}{x}(a,b) - \pdiff{\dlvfc_1}{y}(a,b). \end{align*} This is the expression for the scalar curl that we use for the “microscopic circulation” in Green's theorem. If we rewrite this in terms of the original three-dimensional vector field $\dlvf(x,y,z)$ at the point $(x,y,z)=(a,b,c)$, we obtain the expression for the $z$-component of the curl \begin{align*} \curl\dlvf(a,b,c) \cdot \vc{k} = \pdiff{\dlvfc_2}{x}(a,b,c) - \pdiff{\dlvfc_1}{y}(a,b,c) \end{align*} as promised.
Thread navigation
Multivariable calculus
- Previous: The definition of curl from line integrals
- Next: Introduction to a line integral of a scalar-valued function
Math 2374
Notation systems
Similar pages
- The idea behind Green's theorem
- The definition of curl from line integrals
- A path-dependent vector field with zero curl
- The idea behind Stokes' theorem
- The idea of the curl of a vector field
- Subtleties about curl
- The components of the curl
- Line integrals as circulation
- When Green's theorem applies
- Green's theorem with multiple boundary components
- More similar pages