Elementary discrete dynamical systems biology problems, part 2
Problem 1
Let $x_n$ be the number of fish in generation $n$ in a lake. We'll model the evolution of the fish using Ricker's model of the form \begin{align*} x_{n+1} = 5x_n e^{-x_n}, \end{align*}
The equilibria of this model are $x_n=0$ and $x_n= \ln(5)$.
- Calculate the stability of the equilibria using calculus.
- Confirm the stability through cobwebbing the below graph.
- For any positive initial fish population $x_0$, what will happen to the fish population $x_n$ as $n$ gets large?
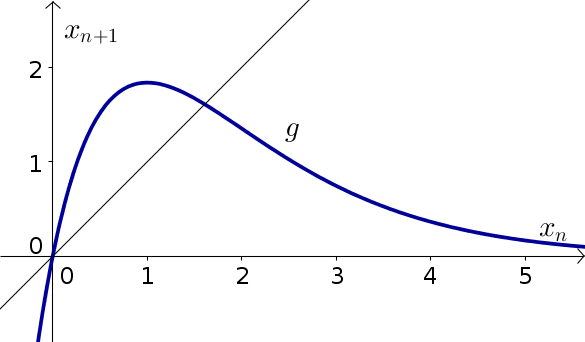
Problem 2
Let $x_n$ be the number of fish in generation $n$ in a lake. We'll model the evolution of the fish using Ricker's model of the form \begin{align*} x_{n+1} = 8x_n e^{-x_n}, \end{align*}
The equilibria of this model are $x_n=0$ and $x_n= \ln(8)$.
- Calculate the stability of the equilibria using calculus.
- Confirm the stability through cobwebbing the below graph.
- If the initial fish population $x_0$ is close to (but not equal to) $\ln(8)$, what will happen to the fish population $x_n$ as $n$ increases?
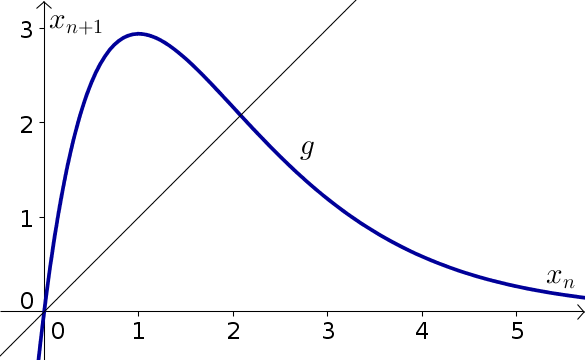
Problem 3
A population of squirrels would be increasing at rate of 50% per year, except that due to a scarcity of acorns, there is only enough food to support 300 squirrels. Therefore, if $s_t$ is the number of squirrels in year $t$, the population evolves according to the dynamical system \begin{align*} s_{t+1} - s_{t} = 0.5 s_t\left(1 - \frac{s_t}{300}\right). \end{align*}
Calculate the equilibria of the dynamical system and their stability. If the initial population is $s_0=400$, what will happen to the population after a long time?
Problem 4
A population of squirrels would be increasing at rate of $r$ per year, except that due to a scarcity of acorns, there is only enough food to support $N$ squirrels. Therefore, if $s_t$ is the number of squirrels in year $t$, the population evolves according to the dynamical system \begin{align*} s_{t+1} - s_{t} = r s_t\left(1 - \frac{s_t}{N}\right). \end{align*}
- Calculate the equilibria of the dynamical system.
- If $r=1.5$, determine the stability of the equilibria.
- If $r=1.5$, $N=500$, and the initial population is $s_0=400$, what will happen to the population after a long time?
- If $r=3$, determine the stability of the equilibria.
- For what range of $r$ is there a stable nonzero equilibrium?
Problem 5
A population of deer is growing exponentially so that in each year the population increases by 20%. In order to keep the population from exploding, a number of deer is harvested annually that is proportional to the square of the population. If $d_t$ is the number of deer in year $t$, the population follows the dynamical system \begin{align*} d_{t+1}=1.2 d_t - c d_t^2 \end{align*} where $c$ is a positive parameter that determines the amount of harvesting.
- Find the equilibria of this system.
- Calculate the stability of the equilibria.
- How does the stability of the equilibria depend on the parameter $c$?
- For what value of $c$ is there a stable equilibrium of 200 deer?
Problem 6
A population of locusts is growing out of control, so that the number of locusts is quadupling each year. In attempt to limit the population, each year a number of locusts is killed that is proportional to the square of the population. If $l_t$ is the number of locusts in year $t$, the population follows the dynamical system \begin{align*} l_{t+1}=4 l_t - c l_t^2 \end{align*} where $c$ is a positive parameter that determines the amount of harvesting.
- Find the equilibria of this system.
- Calculate the stability of the equilibria.
- How does the stability of the equilibria depend on the parameter $c$?
- Will this strategy succeed in bringing the number of locusts to a stable small population?
One you have worked on a few problems, you can compare your solutions to the ones we came up with.
Thread navigation
Elementary dynamical systems
Similar pages
- The idea of a dynamical system
- An introduction to discrete dynamical systems
- Developing an initial model to describe bacteria growth
- Bacteria growth model exercises
- Bacteria growth model exercise answers
- Exponential growth and decay modeled by discrete dynamical systems
- Discrete exponential growth and decay exercises
- Discrete exponential growth and decay exercise answers
- Doubling time and half-life of exponential growth and decay
- Constructing a mathematical model for penicillin clearance
- More similar pages