Math Insight

Solutions to elementary discrete dynamical systems problems, part 2

The following is a set of solutions to the elementary discrete dynamical systems problems, part 2.

Problem 1

1. To find the equilibria, we plug in $x_{n+1}=x_n = E$. \begin{align*} E &= E^2\\ E-E^2 &=0\\ E(1-E) &=0\\ E=0 & \quad \text{or} \quad E=1 \end{align*}

2. To determine the stability of the equilibria, the first step is to write the system as $x_{n+1}=f(x_n)$. In this case, the dynamical system is already in that form, with $f(x)=x^2$. The derivative $f'(x)=2x$, and we evaluate it at the equilibria.

   For $E=0$: $f'(0) = 0$. Since $|f'(0)| \lt 1$, the equilibrium $x_n=0$ is stable.

   For $E=1$: $f'(1) = 2$. Since $f'(1)>1$, the equilibrium $x_n=1$ is unstable.

3. The below cobwebbing confirms that the equilibrium $x_n=0$ is stable and the equilibrium $x_n=1$ is unstable.

   

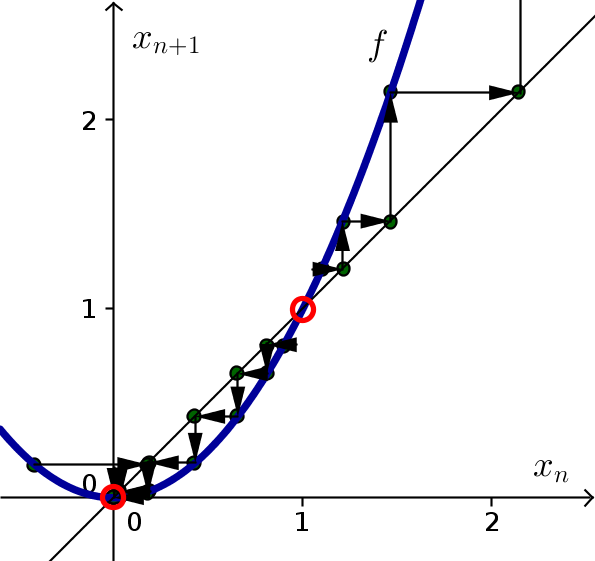
Problem 2

1. To find the equilibria, plug in $y_{t+1}=y_t = E$. \begin{align*} E &= E^3\\ E - E^3 &= 0\\ E(1-E^2) &= 0\\ E(1-E)(1+E) &= 0\\ E=0 \quad \text{or} \quad E &= \pm 1 \end{align*}
2. The dynamical system is already in the form $y_{t+1}=g(y_t)$ where $g(y)=y^3$. Since $g'(y)=3x^2$, we calculate that at the equilibria $g'(0)=0$, $g'(1)=g'(-1)=3$. The equilibrium $y_t=0$ since $|g'(0)|<1$. The equilibria $y_t=1$ and $y_t=-1$ are unstable since $g'(1)>1$ and $g'(-1)>1$.

3. The below cobwebbing confirms that the equilibrium $y_t=0$ is stable and the equilibria $y_t=1$ and $y_t=-1$ are unstable.

   

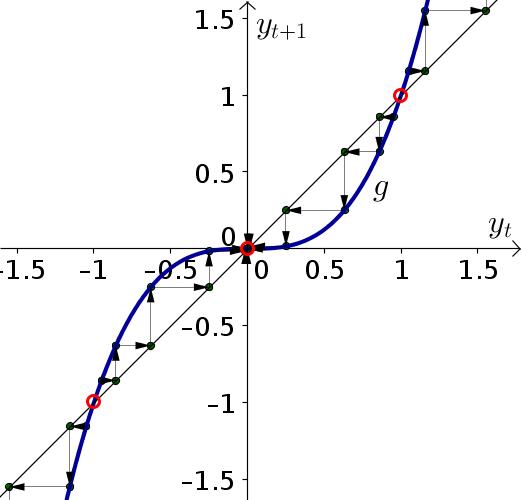
Problem 3

Consider the dynamical system \begin{align*} z_{t+1} -z_t &= z_t(1-z_t) \quad \text{for $t=0,1,2,3, \ldots$} \end{align*}

1. Plug in $z_{t+1}=z_t=E$. \begin{align*} E - E &= E(1-E)\\ 0 &= E(1-E)\\ E &= 0 \quad \text{or} \quad E=1 \end{align*}
2. Need to rewrite system in the form $z_{t+1}=f(z_t)$. Just add $z_t$ to borth sides. \begin{align*} z_{t+1} -z_t &= z_t(1-z_t)\\ z_{t+1} &= z_t + z_t(1-z_t)\\ &= f(z_t) \end{align*} where $f(z)=z+z(1-z)$.

   The derivative of $f$ is \begin{align*} f'(z) &= 1 + 1(1-z) + z(-1)\\ &= 1 + 1-z-z\\ &= 2 -2z. \end{align*}

   Plugging in $z_t=0$: $f'(0) = 2 >1 $, so the equilibrium $z_t=0$ is unstable.

   Plugging in $z_t=1$: $|f'(1)|=0 < 1$, so the equiliibrium $z_t=1$ is stable.

3. The below cobwebbing confirms that the equilibrium $z_t=0$ is unstable and the equilibrium $z_t=1$ is stable.

   

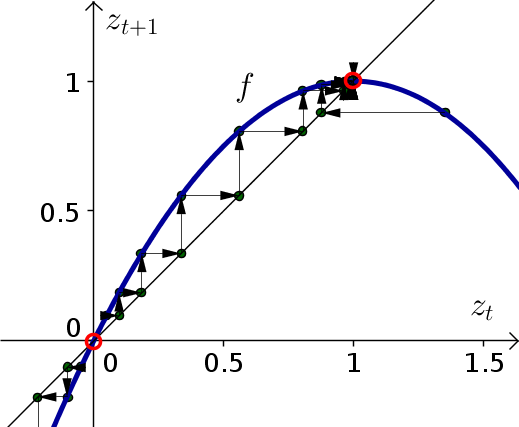
Problem 4

1. Plugging in $w_{n+1}=w_n=E$, \begin{align*} E-E&= 3E(1-E/2)\\ 0 &= 3E(1-E/2)\\ E &=0 \quad \text{or} \quad E=2 \end{align*}
2. We solve for $w_{n+1}$ by adding $w_n$ to both sides of the dynamical system: \begin{align*} w_{n+1} &= w_n + 3w_n(1-w_n/2)\\ &= g(w) \end{align*} where $g(w)=w+3w(1-w/2)$. The derivative is \begin{align*} g'(w)&=1+3(1-w/2)-3w/2\\ &=1 +3 -3w/2-3w/2\\ &= 4 - 3w. \end{align*} Since $g'(0)=4 >1$, the equilibrium $w_n=0$ is unstable. Since $|g'(2)| = |-2| > 1$, the equilibrium $w_n=2$ is also unstable.

Problem 5

1. Let $v_{n+1}=v_n=E$ so that \begin{align*} E - E &= 0.9E(2-E)\\ 0 &= 0.9E(2-E)\\ E &=0 \quad \text{or} \quad E = 2. \end{align*}
2. Adding $v_n$ to both sides: \begin{align*} v_{n+1} &= v_n + 0.9v_n(2-v_n)\\ &= g(v_n) \end{align*} where $g(v) = v+0.9v(2-v)$. The derivative is \begin{align*} g'(v) &= 1 + 0.9(2-v) - 0.9v\\ &=2.8 - 1.8v. \end{align*} Since $g'(0)=2.8 > 1$, the equilibrium $v_n=0$ is unstable. Since $|g'(2)| = |-0.8| = 0.8 < 1$, the equilibrium $v_n=2$ is stable.

Problem 6

1. Let $u_{t+1}=u_t = E$. so that \begin{align*} E - E &= a E(1-E)\\ 0 &= aE(1-E)\\ E &=0 \quad \text{or} \quad E=1 \end{align*}

2. Add $u_t$ to both size to solve for $u_{t+1}$ \begin{align*} u_{t+1} &= u_t+ a u_t(1-u_t)\\ &= f(u) \end{align*} where $f(u) = u+au(1-u)$. The derivative is \begin{align*} f'(u) &= 1 + a(1-u) - au\\ &=1+a -2au \end{align*}

   The equilibrium $u_t=0$ is stable when $|f'(0)|< 1$. Since $f'(0) = 1+a$, this condition is satisfied when $|1+a|<1$. We see that the equilibrium $u_t=0$ is stable when $-2 < a < 0$. It is unstable when $|f'(0)|=|1+a|>1$, i.e., when $a < -2$ or $a>0$.

   The equilibrium $u_t=1$ is stable when $|f'(1)| = |1-a| < 1$, i.e., when $0 < a < 2$. The equilibrium $u_t=1$ is unstable when $|f'(1)| = |1-a| > 1$, i.e., when $a < 0$ or $a > 2$.

Problem 7

Consider the dynamical system \begin{align*} s_{t+1} -s_t &= 0.5s_t(1-s_t/b) \quad \text{for $t=0,1,2,3, \ldots$} \end{align*} where $b$ is a positive parameter.

1. Let $s_{t+1}=s_t = E$. \begin{align*} E - E &= 0.5E(1-E/b)\\ 0 &= 0.5 E(1-E/b)\\ E &=0 \quad \text{or} \quad E=b \end{align*}
2. Write system as \begin{align*} s_{t+1} &=s_t+ 0.5s_t(1-s_t/b)\\ &= h(s) \end{align*} where $h(s) = s+0.5s(1-s/b)$. The derivative is \begin{align*} h'(s) &= 1 + 0.5(1-s/b) - 0.5s/b\\ &= 1.5 - s/b. \end{align*} Since $h'(0) = 1.5 > 1$, the equilibrium $s_t=0$ is unstable. Since $|h'(b)| = |1.5 - 1 |= 0.5 < 1$, the equilibrium $s_t =b $ is stable.
3. The stability of the equilibria does not depend on $b$.