Math Insight

Double integrals as area

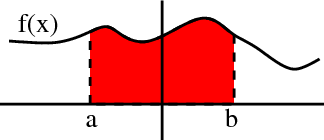
One use of the single variable integral is calculate the area under a curve $f(x)$ over some interval $[a,b]$ by integrating $f(x)$ over that interval.

Sometimes, we use double integrals to calculate area as well. But, the approach is quite different. It's fairly simple to see the trick to accomplish this once you can imagine how to use a single integral to calculate the length of the interval.

What happens if you integrate the function $f(x)=1$ over the interval $[a,b]$? You can calculate that \begin{align*} \int_a^b f(x)dx = \int_a^b 1 dx = x\big|_a^b = b-a. \end{align*} The integral of the function $f(x)=1$ is just the length of the interval $[a,b]$. It also happens to be the area of the rectangle of height 1 and length $(b-a)$, but we can interpret it as the length of the interval $[a,b]$.

We can do the same trick for double integrals. The integral of a function $f(x,y)$ over a region $\dlr$ can be interpreted as the volume under the surface $z=f(x,y)$ over the region $\dlr$. As we did above, we can try the trick of integrating the function $f(x,y)=1$ over the region $\dlr$. This would give the volume under the function $f(x,y)=1$ over $\dlr$. But the integral of $f(x,y)=1$ is also the area of the region $\dlr$. This can be a nifty way of calculating the area of the region $\dlr$. If we let $A$ be the area of the region $\dlr$, we can write this as \begin{align*} A = \iint_\dlr dA. \end{align*}

Example

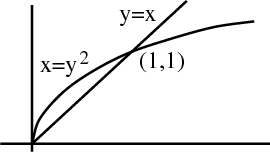
Find area of region bounded by parabola $x=y^2$ and the line $y=x$. The region is pictured below.

Solution: We'll let $y$ go from 0 to 1. Then $x$ goes from $y^2$ to $y$.

The area is \begin{align*} \int_0^1 \int_{y^2}^y dx\, dy &= \int_0^1 \left( \left. x \right|_{x=y^2}^{x=y}\right) dy\\ &= \int_0^1 (y-y^2) dy\\ &= \biggl[\frac{y^2}{2} - \frac{y^3}{3}\biggr]_0^1\\ &=\frac1{2}-\frac1{3} = \frac1{6}. \end{align*}