Introduction to double integrals
Suppose that you knew the hair density at each point on your head and you wanted to calculate the total number of hairs on your head.
In other words, let $(x,y)$ be a point that is $x$ millimeters to the right and $y$ millimeters above some reference point, say your nose. We are assuming that you already know the function $f(x,y)$ that gives hair density in hairs per square millimeter at point $(x,y)$. The following might be a method to use your knowledge of $f(x,y)$ to estimate the number of hairs on your body.
Cut and flatten your skin so it lies in a plane.
(Although this has nothing to do with double integrals, brain mappers and cartographers face similar problems. To map the brain or the surface of the earth, one looks for ways to flatten these surfaces into a plane.)
Divide your skin into small rectangles of width $\Delta x$ and height $\Delta y$.
Label each rectangle according to row $i$ and column $j$. For rectangle $ij$, pick some point in the rectangle, and call it $(x_{ij},y_{ij})$. Since you know your hair density function, you can look up the hair density of that point. It is simply $f(x_{ij},y_{ij})$.
Label each rectangle by the number $f(x_{ij},y_{ij})$.
-
If the hair density were constant in each rectangle, the number of hairs in rectangle $ij$ would be $f(x_{ij}, y_{ij})$ times the area of the rectangle. The area of the rectangle is simply its width ($\Delta x$) times its height ($\Delta y$), i.e., the area is $\Delta x \Delta y$. Hence, the number of hairs in the rectangle is approximately $f(x_{ij},y_{ij})\Delta x \Delta y$.
To estimate the total number of hairs on your head, you can add up the (approximate) number of hairs in each rectangle. Using the above result, your estimate for the total number of hairs is \begin{align*} \sum_{i,j} f(x_{ij},y_{ij})\Delta x \Delta y, \end{align*} where the sum is over all rectangles.
If in the above picture, each rectangle were 75 millimeters wide and 65 millimeters high, then the resulting estimate of the total number of hairs would be $(9+9+8+17+9+3+1+1+11+8+10+8+1+2+3+8+7+2+5+3) \cdot 75 \cdot 65 = 609,375$.
The above result is only a rough estimate because it assumed that the hair density was constant over each rectangle. You may also have noticed that additional errors are introduced around the edges of your skin, where some rectangles are only partly filled with skin. You can increase your accuracy by decreasing the size of each rectangle (i.e., decreasing $\Delta x$ and $\Delta y$). Of course, to cover your whole head, you'll have to increase the number of rectangles as you decrease their size.
To be really accurate, you should let the size of the rectangles go to zero (and the number of rectangles go to infinity). In other words, you should take the limit where $\Delta x \to 0$ and $\Delta y \to 0$.
As long as $f(x,y)$ is a continuous function, this procedure will converge to a single number, which would be the actual number of hairs on your head. \begin{align*} \text{Number of hairs on head} = \lim_{\Delta x, \Delta y \to 0} \sum_{i,j} f(x_{ij}, y_{ij}) \Delta x \Delta y \end{align*}
We can put this into math terms. When we took the limit as $\Delta x \to 0$ and $\Delta y \to 0$, we ended up with the definite integral of the function $f$ over your head. If we denote by $\dlr$ the region of the plane that your skin occupied, then we write this integral as \begin{align*} \iint_\dlr \, f(x,y) dA = \lim_{\Delta x, \Delta y \to 0} \sum_{i,j} f(x_{ij}, y_{ij}) \Delta x \Delta y. \end{align*}
We refer to this integral as the double integral of $f$ over $\dlr$.
The sums of step 5 are the Riemann sums that approximate the integral. The integral is the limit of the Riemann sums as the size of the rectangles goes to zero. This is exactly the way you defined the integral in one-variable calculus.
You can read how we can interpret the double integral as volume underneath a surface, just like you could interpret the regular one-variable integral as area under a curve. In this case, we can also visualize the Riemann sum defining the integral as the volume of many boxes, as illustrated in the below applet. (More details on this volume interpretation and this applet can be viewed on this page.)
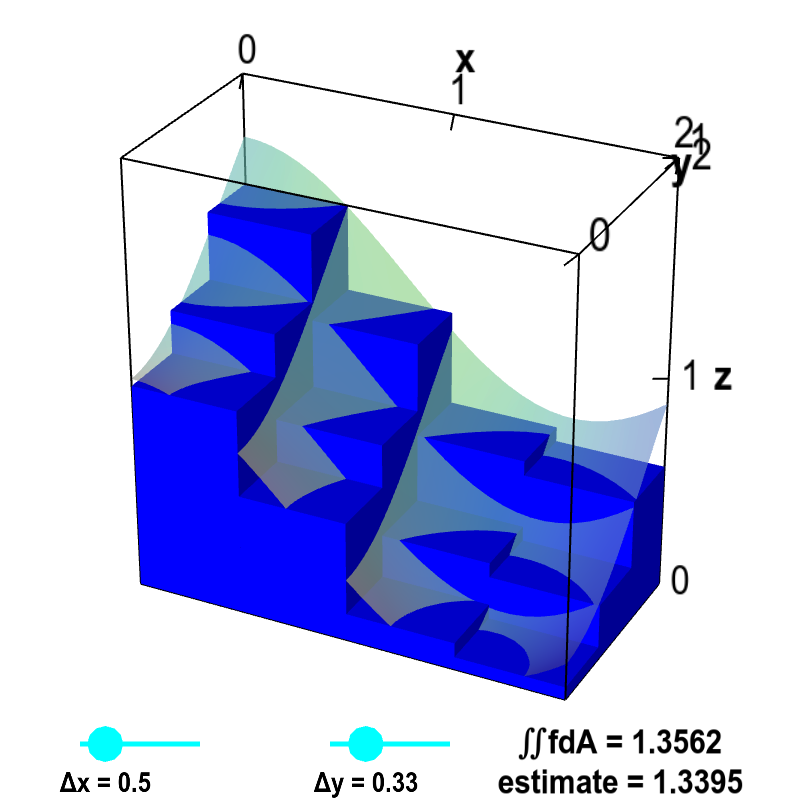
Applet loading
Double integral Riemann sum. The volume of the small boxes illustrates a Riemann sum approximating the volume under the graph of $z=f(x,y)$, shown as a transparent surface. The surface is the graph of the function $f(x,y)=\cos^2 x + \sin^2 y$. The volume is computed over the region $D$ defined by $0 \le x \le 2$ and $0 \le y \le 1$. Therefore, the actual volume is the double integral $\iint_D f\,dA$. The volume of the boxes is $$\sum_{i,j} f(x_{i},y_{j})\Delta x \Delta y$$ where $x_i$ is the midpoint of the $i$th interval along the $x$-axis and $y_j$ is the midpoint of the $j$th interval along the $y$-axis. Drag the points on the sliders to change $\Delta x$ and $\Delta y$ as well as the number of intervals along each axis. As $\Delta x$ and $\Delta y$ approach zero, the volume of the boxes (labeled as “estimate”) approaches the actual volume of the integral $\iint_D f\,dA$.
I don't have good examples (other than the above hair-counting example) on computing double integrals this way, as this is not how we typically compute them. Instead, this page is about how we define a double integral. We have better ways to compute double integrals (that is, unless you are a computer, in which case chopping up the domain in pieces and computing a sum as an approximation to an integral works pretty well).
You can also read examples of computing double integrals using the method in which those of us who are not computers typically use, which is something called an iterated integral.
Thread navigation
Multivariable calculus
Math 2374
Similar pages
- Double integrals as iterated integrals
- Double integral examples
- Double integrals as volume
- Examples of changing the order of integration in double integrals
- Double integrals as area
- Double integrals where one integration order is easier
- Introduction to changing variables in double integrals
- Area calculation for changing variables in double integrals
- Double integral change of variable examples
- The integrals of multivariable calculus
- More similar pages


