Stokes' theorem examples
Example 1
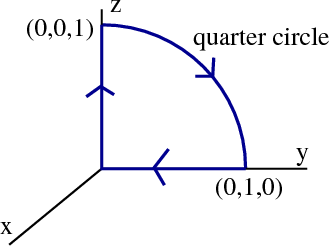
Let $\dlc$ be the closed curve illustrated below.
For $\dlvf(x,y,z) = (y,z,x)$, compute \begin{align*} \dlint \end{align*} using Stokes' Theorem.
Solution: Since we are given a line integral and told to use Stokes' theorem, we need to compute a surface integral \begin{align*} \sint{\dls}{\curl \dlvf}, \end{align*} where $\dls$ is a surface with boundary $\dlc$. We have freedom to choose any surface $\dls$, as long as we orient it so that $\dlc$ is a positively oriented boundary.
In this case, the simplest choice for $\dls$ is clear. Let $\dls$ be the quarter disk in the $yz$-plane.
Given the orientation of the curve $\dlc$, we need to choose the surface normal vector $\vc{n}$ to point in which direction? By the right hand rule criterion, the normal vector should point toward the negative side of the $x$-axis.
We need to calculate the curl of $\dlvf$. We can calculate the curl as using the notation \begin{align*} \curl(\dlvf) &= \nabla \times \dlvf = \nabla \times (y,z,x)\\ & = \left| \begin{array}{ccc} \vc{i} & \vc{j} & \vc{k}\\ \displaystyle \pdiff{}{x} & \displaystyle \pdiff{}{y} & \displaystyle \pdiff{}{z}\\ y & z & x \end{array} \right|\\ &= \vc{i} \left(\pdiff{}{y} x - \pdiff{}{z} z\right) -\vc{j} \left(\pdiff{}{x} x - \pdiff{}{z}y\right)\\ &\quad+\vc{k} \left(\pdiff{}{x} z - \pdiff{}{y}y\right)\\ &= \vc{i} (-1) - \vc{j} (1) + \vc{k} (-1)\\ &= (-1, -1, -1) \end{align*}
Next, parameterize the surface (the quarter disk) by \begin{align*} \dlsp(r,\theta) = (0, r\cos\theta, r\sin\theta) \end{align*} for $0 \le r \le 1$ and $0 \le \theta \le \pi/2$.
Calculate the normal vector (we don't need to normalize it to the unit normal vector $\vc{n}$): \begin{align*} \pdiff{\dlsp}{r} &= (0, \cos\theta, \sin\theta)\\ \pdiff{\dlsp}{\theta} &= (0, -r\sin\theta, r\cos\theta)\\ \pdiff{\dlsp}{r} \times \pdiff{\dlsp}{\theta} &= \vc{i} (r \cos^2\theta + r \sin^2\theta) = r \vc{i} \end{align*}
Is the surface oriented properly? The normal vector points in the positive x-direction. But we need it to point it negative x-direction. Therefore, the surface is not oriented properly if we were to choose this normal vector.
To orient the surface properly, we must instead use the normal vector $\displaystyle\pdiff{\dlsp}{\theta} \times \pdiff{\dlsp}{r} = -r \vc{i}$.
At this point, we can already see that the integral $\sint{\dls}{\curl \dlvf}$ should be positive. The vector field $\curl \dlvf = (-1,-1,-1)$ and the normal vector $(-r,0,0)$ are pointing in a similar direction.
Now, we have all pieces together to compute the integral. \begin{align*} \dlint &=\sint{\dls}{\curl \dlvf}\\ &= \psintrnro{0}{1}{0}{\pi/2}{\curl \dlvf}{\dlsp}{r}{\theta}\\ &=\int_0^1 \int_0^{\pi/2} (-1,-1,-1) \cdot (-r, 0, 0) d\theta\, dr\\ &=\int_0^1 \int_0^{\pi/2} r d\theta\,dr = \frac{\pi}{4} \end{align*}
Double-check example 1
Just for verification, we can compute the line $\dlint$ directly.
We need to parametrize $\dlc$. We'll do it by dividing $\dlc$ into three parts.
We'll use the fact that \begin{align*} \dlint =\lint{\dlc_1}{\dlvf} + \lint{\dlc_2}{\dlvf} + \lint{\dlc_3}{\dlvf} \end{align*}
Recall $\dlvf(x,y,z) = (y,z,x)$
First we'll compute the integral over $\dlc_1$. Parameterize it by \begin{align*} \dllp(t) &= (0,0,t), \qquad 0 \le t \le 1. \end{align*} Since $\dllp'(t)=(0,0,1)$, we compute that \begin{align*} \dlvf(\dllp(t)) \cdot \dllp'(t) &= \dlvf(0,0,t) \cdot (0,0,1)\\ &= (0,t,0) \cdot (0,0,1)\\ &=0 \end{align*} Therefore, \begin{align*} \lint{\dlc_1}{\dlvf} &= \plint{0}{1}{\dlvf}{\dllp} =0. \end{align*}
The integral for $\dlc_3$ is similar. \begin{align*} \lint{\dlc_3}{\dlvf} = 0 \end{align*}
Last, we'll compute the integral over $\dlc_2$. Parameterize $\dlc_2$ as \begin{align*} \dllp(t) &= (0,\sin t,\cos t), \qquad 0 \le t \le \pi/2, \end{align*} so that $\dllp'(t) = (0, \cos t, -\sin t)$. We then compute \begin{align*} &\lint{\dlc_2}{\dlvf} = \plint{0}{\pi/2}{\dlvf}{\dllp} \\ &=\int_0^{\pi/2}\dlvf(0,\sin t,\cos t) \cdot (0, \cos t,-\sin t)dt\\ &=\int_0^{\pi/2} (\sin t, \cos t,0) \cdot (0, \cos t,-\sin t)dt\\ &=\int_0^{\pi/2} \cos^2t \, dt\\ &=\int_0^{\pi/2} \frac{1+\cos 2t}{2} dt\\ &= \frac{t}{2} + \left.\left.\frac{\sin 2t}{4} \right|_0^{\pi/2}\right. = \frac{\pi}{4}. \end{align*}
Therfore, \begin{align*} \dlint = \frac{\pi}{4} \end{align*} in agreement with our Stokes' theorem answer.
Example 2
We often present Stoke's theorem problems as we did above. We give a curve $\dlc$ and expect you to compute the surface integral over some surface $\dls$ with boundary $\dlc$. In general, one can pick many surfaces. (See this applet.) But, sometimes, there is a surface that is “obviously” the best one.
One special case where this is relatively easy is when $\dlc$ lies in a plane. This is especially easy when that plane is parallel to a coordinate plane, as in the following example. (We won't work out this example, but just discuss how to choose $\dls$).
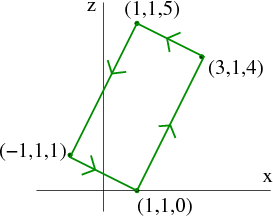
Let's say you want to use Stokes' theorem to compute $\dlint$ where $\dlc$ is polygon path connecting the following points: (1,1,0), (3,1,4), (1,1,5), (-1,1,1)
Does this curve lie in a plane? Yes, in the plane $y=1$. The figure below is just the plane $y=1$.
If one coordinate is constant, then curve is parallel to a coordinate plane. (The $xz$-plane for above example). For Stokes' theorem, use the surface in that plane. For our example, the natural choice for $\dls$ is the surface whose $x$ and $z$ components are inside the above rectangle and whose $y$ component is 1.
Example 3
In other cases, a surface is given explicitly in the problem.
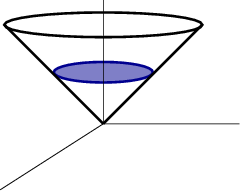
Compute $\dlint$, where $\dlc$ is the curve in which the cone $z^2=x^2+y^2$ intersects the plane $z=1$. (Oriented counter clockwise viewed from positive $z$-axis).
\begin{align*} \dlint = \sint{\dls}{\curl \dlvf} \end{align*} for what surface $\dls$?
In this case, there are two natural choices for the surface. You could use the portion of the plane or the portion of the cone illustrated below.
Let $P$ be the portion of the plane $z=1$ with $x^2+y^2 < 1$ with upward pointing normal. Let $Q$ be the portion of the cone $z^2=x^2+y^2$ with $0 < z < 1$ with upward angling normal.
How do $\sint{P}{\curl \dlvf}$ and $\sint{Q}{\curl \dlvf}$ compare? They are the same. (For both surfaces, $\dlc$ is a positive oriented boundary.)
Continue example: Let \begin{align*} \dlvf(x,y,z) = \left(\sin x - \frac{y^3}{3}, \cos y + \frac{x^3}{3}, xyz \right) \end{align*} Compute $\dlint$.
One can show that $\curl(\dlvf) = (xz,-yz,x^2+y^2)$.
Use surface $P$, parameterized by \begin{align*} \dlsp(r,\theta) = (r \cos\theta, r\sin\theta, 1) \end{align*} for $0 \le r \le 1, 0 \le \theta \le 2\pi$. Then normal vector is \begin{align*} \pdiff{\dlsp}{r} \times \pdiff{\dlsp}{\theta} = (0,0,r), \end{align*} which points in the correct direction, as mentioned above. \begin{align*} \sint{P}{\curl \dlvf} &=\int_0^1 \int_0^{2\pi} \curl(\dlvf(r\cos\theta,r\sin\theta,1)) \cdot (0,0,r) d\theta dr \\ &=\int_0^1 \int_0^{2\pi} (r\cos\theta, -r\sin\theta, r^2) \cdot (0,0,r) d\theta\, dr \\ &= \int_0^1 \int_0^{2\pi} r^3 d\theta\, dr\\ &= \int_0^1 2\pi r^3 dr = \frac{\pi}{2} \end{align*}
