The ellipsoid

Equation: $\displaystyle\frac{x^2}{A^2}+\frac{y^2}{B^2} + \frac{z^2}{C^2} = 1$

Just as an ellipse is a generalization of a circle, an ellipsoid is a generalization of a sphere. In fact, our planet Earth is not a true sphere; it's an ellipsoid, because it's a little wider than it is tall.

As you can verify below, all of the cross sections of an ellipsoid are ellipses. The applet shows an ellipsoid where $A=3$, $B=2$, and $C=1$. Looking at the graph, this gives you a hint about how the constants affect the surface. An ellipsoid centered at the origin stretches out $A$ units in the positive and negative $x$ direction; $B$ units in the positive and negative $y$ direction; and $C$ units in the positive and negative $z$ direction.

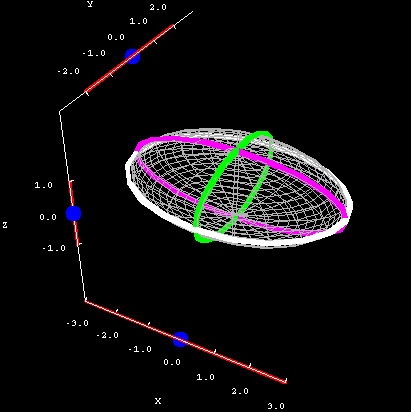
Ellipsoid cross sections. The ellipsoid $\frac{x^2}{3^2}+\frac{y^2}{2^2} + z^2 = 1$ is plotted along with its cross sections. You can drag the blue points on the sliders to change the location of the different types of cross sections.

More information about applet.

What this means is that an ellipsoid is probably the easiest quadric surface to draw accurately. (Or, if your drawing skills are like mine, you at least know what it should look like, even if the actual drawing is somewhat lacking!)

You can interactively adjust the values of $A$, $B$, and $C$ in the second applet, below. Notice that you can get everything from a sphere to a nearly flat pancake.

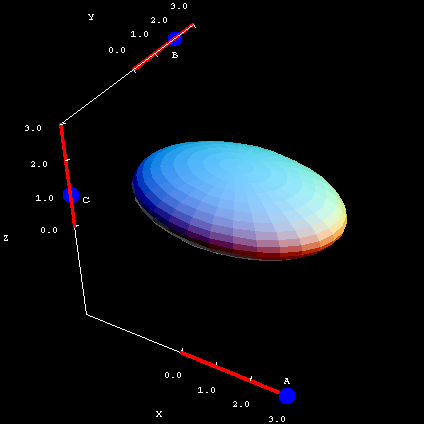
Ellipsoid coefficients. The ellipsoid $\frac{x^2}{A^2}+\frac{y^2}{B^2} + \frac{z^2}{C^2} = 1$ is plotted. You can drag the blue points on the sliders to change the coefficients $A$, $B$, and $C$.

More information about applet.

Here are some things which deserve a little thought on your part:

What needs to happen for an ellipsoid to be a sphere?
The sliders don't actually go all the way to 0. Make the values as small as you can and zoom in to verify this; you'll find you have a very small sphere. (Its radius is 0.1, as it happens.) Why didn't I make the sliders go all the way to 0?
If you want to see an interesting effect, maximize all of the sliders and zoom in (press shift, then click and drag down) until you're inside the ellipsoid. You can rotate around and look at the interior of the surface.