Triple integral change of variables story
Changing variables in triple integrals is nearly identical to changing variables in double integrals. You can view this story as a second chance to understand the basics underlying a change of variables. You can also read a more traditional introduction to changing variables in triple integrals.
Imagine that you are an engineer designing a new electrode tip that will be used to monitor brain activity in people with epilepsy. The end product will be an array of electrodes that will be implanted in the area of a patient's brain where doctors believe the epileptic seizures begin. Once the array of electrodes is implanted in the brain, doctors will be able to monitor the brain's activity before and during a seizure to pinpoint exactly where the seizure begins.
Currently, for severe cases of epilepsy that don't respond to other treatment, the recommended treatment is removing the small part of brain tissue that starts the seizure. Since doctors want to remove as little of the brain as possible, implanting electrode arrays is necessary to find exactly what part of the brain is causing the trouble.
You, however, are working with a team of scientists looking for methods to stop the seizure that don't involve removing parts of the brain. The idea is the following. The electrode arrays can detect patterns of brain activity that signal the seizure is about to begin. What if one can use the electrodes to disrupt that pattern of activity so it doesn't develop into a full blown epileptic seizure? If one passes small pulses of current through the electrodes with the right timing, the hope is that a seizure can be avoided.
With this goal and many other technical requirements in mind, you have developed a prototype electrode tip whose shape is given by the solid $\dlv$ diagrammed below. You have optimized the electrical properties of the electrode tip both through developing the shape $\dlv$ and through incorporating different metal alloys along different parts of the electrode.

Applet loading
A three dimensional domain of an electode trip. The solid $\dlv$ represents a tip of an electrode.
You are quite excited about your new design. You show it to the chief scientist on the project. She likes your design, but has one concern. She wants you to calculate the total charge that may build up on the electrode to make sure it doesn't reach unsafe levels.
From the metal composition of your electrode tip and the information the chief scientist gives you about the current, you quickly calculate $g(x,y,z)$, the charge density at each point $(x,y,z)$ within the electrode tip. To find the total charge, all you need to do is calculate the triple integral \begin{align*} \text{total charge } = \iiint_\dlv g(x,y,z) \, dV, \end{align*} where $\dlv$ is the solid representing the electrode tip.
You struggle with calculating the integral, but, especially given the complicated shape of the electrode, you find that the integral is too difficult to solve directly. Then, you remember something you learned in your multivariable calculus course: changing variables in triple integrals.
Step 1: Integrate over new region $\dlv^*$
Instead of trying to directly integrate $g(x,y,z)$ over $\dlv$, you realize you could solve your problem by finding a change of variables \begin{align*} (x,y,z) = \cvarf(\cvarfv,\cvarsv,\cvartv) \end{align*} that maps a simpler solid $\dlv^*$ onto the complicated solid $\dlv$. Then, rather than integrating over $\dlv$, you could integrate over $\dlv^*$.
After a long night's worth of calculations, you come up with a function $\cvarf(\cvarfv,\cvarsv,\cvartv)$ that looks promising. The effect of the function $\cvarf$ is demonstrated below. The function $\cvarf$ maps a simple solid $\dlv^*$ (shown in the first panel, below) in $(\cvarfv,\cvarsv,\cvartv)$-space to the electrode tip $\dlv$ (shown in the second panel, below) in $(x,y,z)$-space. We often say that $\cvarf(\cvarfv,\cvarsv,\cvartv)$ parametrizes $\dlv$ for $(\cvarfv,\cvarsv,\cvartv)$ in $\dlv^*$.
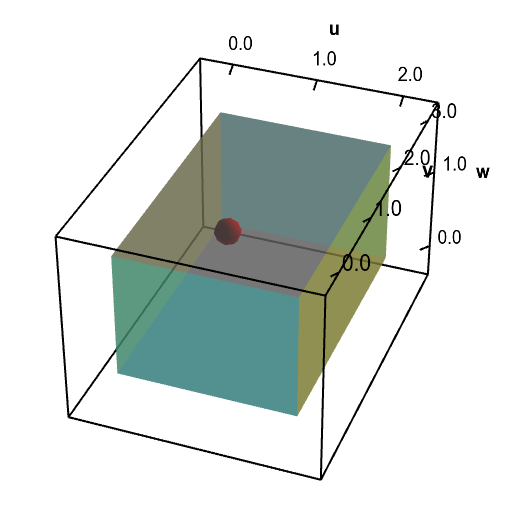
Applet loading

Applet loading
A change of variables for an electrode tip domain. A change of variables $\cvarf$ maps a rectangular solid $\dlv^*$ (first panel) onto the electrode tip $\dlv$ (second panel). You can explore the mapping by moving with the mouse the red point in $\dlv^*$, which represents the point $(\cvarfv,\cvarsv,\cvartv)$, or the point blue point in $\dlv$, which represents the point $(x,y,z)$. When you move one point, the other point moves to reflect the mapping so that $(x,y,z)= \cvarf(\cvarfv,\cvarsv,\cvartv)$.
Step 2: Compose function $g$ with change of variables function $\cvarf$.
Since it is so late after you finished finding $\cvarf(\cvarfv,\cvarsv,\cvartv)$ and you are tired, you almost start to integrate $g$ directly over the solid $\dlv^*$. Fortunately, you realize that such a procedure doesn't make sense because $g$ is a function of $(x,y,z)$ and hence is defined over the electrode tip $\dlv$. Since it is not a function of $(\cvarfv,\cvarsv,\cvartv)$, you can't integrate $g$ over the solid $\dlv^*$ in $(\cvarfv,\cvarsv,\cvartv)$-space. At this point, you are too tired to figure out what you were supposed to do, so you go to bed without finishing your calculation of what the total charge on the electrode would be. You sleep fitfully, dreaming of electrodes that were charged to dangerous levels attacking you.
The next morning, you wake up still groggy, but immediately realize the solution to your problem. Although $g(x,y,z)$ is defined only on your electrode $\dlv$, you can simply compose $g(x,y,z)$ with $\cvarf(\cvarfv,\cvarsv,\cvartv)$ to obtain the function $g(\cvarf(\cvarfv,\cvarsv,\cvartv))$ that is defined in terms of $(\cvarfv,\cvarsv,\cvartv)$. For a given point $(\cvarfv,\cvarsv,\cvartv)$ (shown by the red point, above), the composition $g(\cvarf(\cvarfv,\cvarsv,\cvartv))$ gives the density at the point $(x,y,z)=\cvarf(\cvarfv,\cvarsv,\cvartv)$ (shown by the blue point, above) on the electrode $\dlv$. By integrating $g(\cvarf(\cvarfv,\cvarsv,\cvartv))$ over the solid $\dlv^*$ in $(\cvarfv,\cvarsv,\cvartv)$-space, you will integrate $g(x,y,z)$ over the solid $\dlv$ and compute the total charge. You feel pretty smug that you had this realization even before breakfast and coffee.
Step 3: Include a factor to account for change in volume
Unfortunately, you are still too groggy after your fitful sleep to remember everything you learned in multivariable calculus. You completely forget that $(x,y,z)=\cvarf(\cvarfv,\cvarsv,\cvartv)$ will change volume in $\dlv^*$ compared to volume in $\dlv$. Without compensating for this effect of the map $\cvarf$, your calculations assume that volume in $\dlv$ is the same as volume in $\dlv^*$.
Glancing at the above diagram is enough to guess what the result of this error might be. The volume of $\dlv^*$ is larger than the volume of $\dlv$. Remember that total charge equals charge density times volume. If one uses the correct charge density $g$ of the electrode but multiplies by volume in $\dlv^*$ rather than volume in $\dlv$, the calculation for the total charge should be larger than the correct answer. If, for example, $\dlv^*$ was uniformly twice as large as $\dlv$, then this incorrect calculation for total charge would give an answer that was twice the actual value.
Not realizing this mistake, you proceed with your incorrect calculation and integrate $g(\cvarf(\cvarfv,\cvarsv,\cvartv))$ over $\dlv^*$ without compensating for change in volume. Your result makes you so upset that you kick the table in anger, hurting your foot and spilling your coffee all over your calculations. But at that point, you don't care. You rip up your coffee-soaked notes and limp back to bed to cry. Your design is useless. The total charge on your electrode is much too large. Your hard work is more likely to fry people's brains than help them overcome epilepsy. Or so you think.
Once you stop crying, you discover that your throbbing foot has helped lift your grogginess and your mind is actually becoming clear. Finally, you remember the strict admonition of your calculus professor to never forget to compensate for change in volume when changing variables. You realize that maybe your electrode won't cook people's brains and you might be able to salvage your design.
You grab a fresh piece of paper, race back to your table, and find a dry spot on your table to work. You first sketch the following diagram to show how dividing $\dlv^*$ into little boxes divides $\dlv$ into small pieces. The diagram helps you visualize how changing variables changes volume. You see that, especially around the critical tip of the electrode, the volume in $\dlv$ is much smaller than the volume in $\dlv^*$. This gives you hope that less charge may build up on the electrode than you originally calculated.

Applet loading
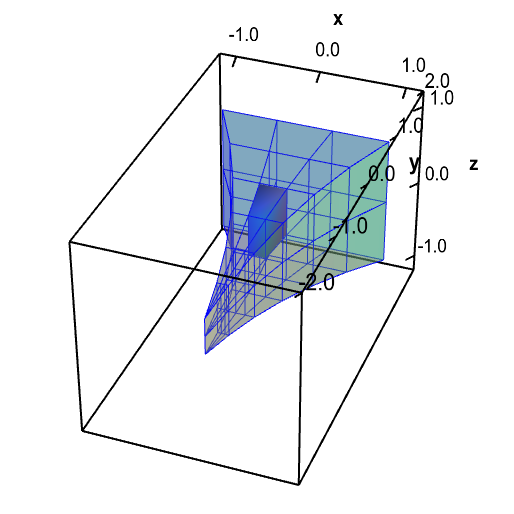
Applet loading
A change of variables for an electrode tip domain changes volume. A change of variables $\cvarf$ maps a rectangular solid $\dlv^*$ (first panel, in red) onto the the electrode tip $\dlv$ (second panel, in blue). It maps each small region of $\dlv^*$ onto a region of a different size in $\dlv$. You can move the highlighted red region in $\dlv^*$ and the highlighted blue region in $\dlv$ by dragging them with your mouse. As you move one region, the corresponding region in the other domain is highlighted. Notice that the red region has a different volume than the corresponding blue region. Especially when the blue region is near the electrode tip, the highlighted blue region is much smaller than the red region.
You realized that to calculate the integral \begin{align*} \iiint_\dlv g(x,y,z) \, dV, \end{align*} as an integral over $\dlv^*$ rather than $\dlv$, you need to make sure that $dV$ still represents volume in $\dlv$ and not volume in $\dlv^*$. Instead of replacing $dV$ with $d\cvarfv~d\cvarsv~d\cvartv$, as you originally did, you must replace $dV$ with $| \det \jacm{\cvarf}(\cvarfv,\cvarsv,\cvartv)| ~d\cvarfv~d\cvarsv~d\cvartv$. Just like for changing variables in double integrals, the absolute value of the determinant of the partial derivative matrix of $\cvarf(\cvarfv,\cvarsv,\cvartv)$, sometimes called the volume expansion factor, accounts for the stretching and shrinking of $\cvarf(\cvarfv,\cvarsv,\cvartv)$ as it maps $\dlv^*$ onto $\dlv$.
You finally calculate your integral correctly as \begin{align*} \iiint_\dlv g(x,y,z) \, dV = \iiint_{\dlv^{\textstyle *}} g(\cvarf(\cvarfv,\cvarsv,\cvartv)) | \det \jacm{\cvarf}(\cvarfv,\cvarsv,\cvartv)| ~d\cvarfv~d\cvarsv~d\cvartv. \end{align*}
You happily discover that the total charge on your electrode meets acceptable limits and that your work is not destined for the trash can! Overjoyed, you jump into the shower, don your best suit, and rush to work. At the office, you slowly walk past the chief scientist who asks if you determined the charge that will build up on your electrode. You casually mention that the charge is well within acceptable limits. You return to your desk to work on the next stage of the design, vowing never to forget anything else you learned in your multivariable calculus course.
You can also read an introduction to changing variables in triple integrals from a different perspective, as well as more details on the calculation behind the volume expansion factor. You can read examples about changing variables in triple integrals here.
Thread navigation
Multivariable calculus
- Previous: Illustrated example of changing variables in double integrals
- Next: Introduction to changing variables in triple integrals
Math 2374
Notation systems
Similar pages
- Introduction to changing variables in triple integrals
- Volume calculation for changing variables in triple integrals
- Introduction to triple integrals
- Triple integral examples
- Area calculation for changing variables in double integrals
- Triple integral change of variable examples
- Illustrated example of changing variables in double integrals
- The shadow method for determining triple integral bounds
- The cross section method for determining triple integral bounds
- Introduction to changing variables in double integrals
- More similar pages