The double cone
The double cone
Equation: $z^2=Ax^2+By^2$
The double cone is a very important quadric surface, if for no other reason than the fact that it's used to define the so-called conics -- ellipses, hyperbolas, and parabolas -- all of which can be created as the intersection of a plane and a double cone. See any PreCalculus or Calculus textbook for pictures of this.
The vertical cross sections of a double cone are hyperbolas, while the horizontal cross sections are ellipses. The below applet shows the cone where $A=B=1$.
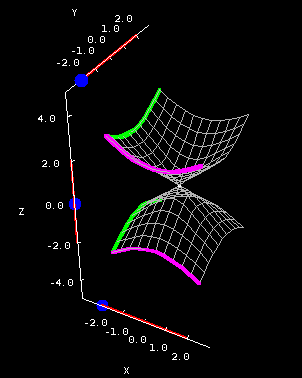
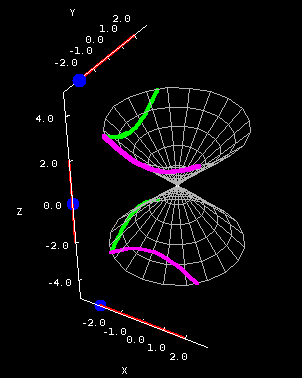
Double cone cross sections. The double cone $z^2=x^2+y^2$ is plotted on a square domain $-2 \le x \le 2, -2 \le y \le 2$ in the first panel and on the circular domain $x^2+y^2 \le 8$ in the second panel. You can drag the blue points on the sliders to change the location of the different types of cross sections.
Look back at the equation for the double cone. Sometimes we manipulate it to get a single cone. If we solve for $z$, we end up with a plus/minus sign in front of a square root. The positive square root represents the top of the cone; the negative square root gives you an equation for the bottom. Be careful if somebody says “cone” without elaborating; they might mean “double cone” or “single cone,” depending on the context.
Roughly speaking, the constants $A$ and $B$ determine how “steep” the cone is in the $x$ and $y$ direction, respectively. You can get a feel from this in the second applet, below, which at the left shows the portion of a cone for which $x$ and $y$ are between -1 and 1. In the right panel, the domain is a disk, and it shows the portion of the cone for which $-4 \le z \le 4.$
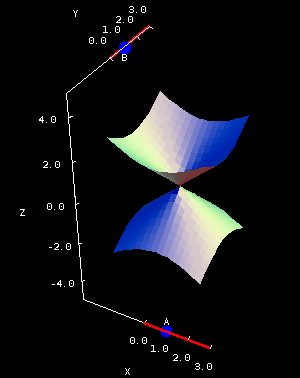
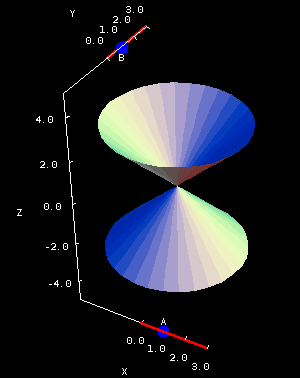
Double cone coefficients. The cone $z^2=Ax^2+By^2$ is plotted over the square domain $-2 \le x \le 2, -2 \le y \le 2$ in the first panel. In the second panel, the same cone is plotted over the elliptical domain for which $-3 \le z \le 3$, a domain whose shape depends on the coefficients $A$ and $B$. You can drag the blue points on the sliders to change $A$ and $B$, which are constrained to be positive.
After you've played around with the examples for awhile, see if you can answer the following questions:
- Why aren't any of the vertical or horizontal cross sections parabolas?
- Explain what happens when either $A=0$ or $B=0$. Why don't you get a cone?
- Similarly, what are the cross sections given by $x=0$ or $y=0$? Are these hyperbolas?
List of quadric surfaces
Thread navigation
Interactive Gallery of Quadric Surfaces
- Previous: The ellipsoid
- Next: The hyperboloid of one sheet