The hyperboloid of two sheets
The hyperboloid of two sheets
Equation: $\displaystyle-\frac{x^2}{A^2}-\frac{y^2}{B^2} + \frac{z^2}{C^2} = 1$
The hyperboloid of two sheets looks an awful lot like two (elliptic) paraboloids facing each other. It's a complicated surface, mainly because it comes in two pieces. All of its vertical cross sections exist -- and are hyperbolas -- but there's a problem with the horizontal cross sections.
This problem is evident in the below applet, where you can see the cross sections of $$-x^2-y^2+z^2 = 1.$$
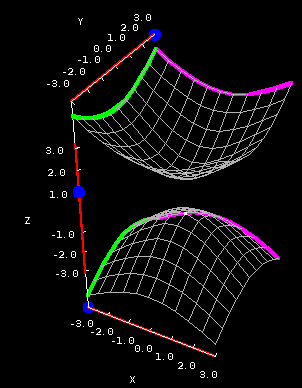
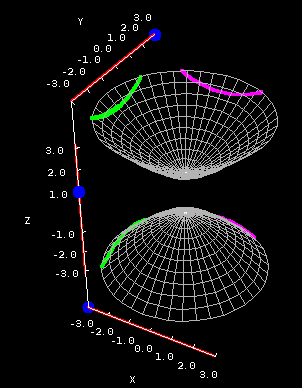
Hyperboloid of two sheets cross sections. The hyperboloid of two sheets $-x^2-y^2+z^2 = 1$ is plotted on both square (first panel) and circular (second panel) domains. You can drag the blue points on the sliders to change the location of the different types of cross sections.
The horizontal cross sections are generally ellipses, except that there are no horizontal cross sections when $z$ is between -1 and 1. To see why this happens, look at the equation above. Suppose $z=0$. Then the left hand side is definitely negative, but the right hand side is definitely positive. There's no way to fix this, so the cross section simply doesn't exist!
Here's a hint about telling the two kinds of hyperboloids apart: look at the cross sections $x=0$, $y=0$, and $z=0$. If they exist, then it's a hyperboloid of one sheet. (Go back to that page and convince yourself that its cross sections all exist.) If you end up with something negative equal to something positive, then you've got a two-sheeter.
By now you probably expect that larger values of $A$, $B$, and $C$ make for a much steeper surface, right? Wrong! It's true that making $C$ larger will have a dramatic effect on the surface, but use the below applet to find out what happens when you increase $A$ and $B$. Surprised?
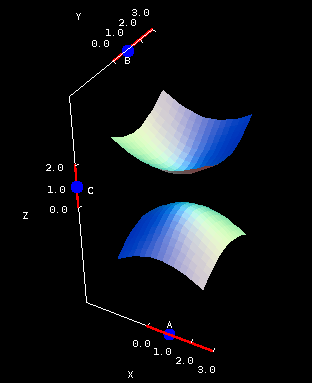
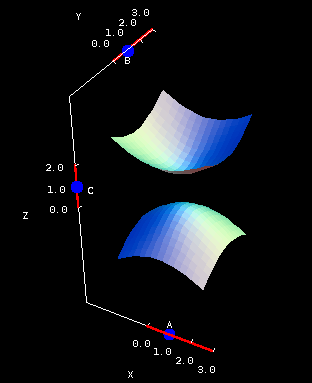
Hyperboloid of two sheets coefficients. The hyperboloid of two sheets $-\frac{x^2}{A^2}-\frac{y^2}{B^2} + \frac{z^2}{C^2} = 1$ is plotted on both square (first panel) and circular (second panel) domains. You can drag the blue points on the sliders to change the coefficients $A$, $B$, and $C$.
Go back to the equation and figure out why larger values of $A$ and $B$ make the hyperboloid flatter, not steeper.
Does there always need to be a gap between the two sheets, or could they touch?
List of quadric surfaces
- Elliptic paraboloid
- Hyperbolic paraboloid
- Ellipsoid
- Double cone
- Hyperboloid of one sheet
- Hyperboloid of two sheets
Thread navigation
Interactive Gallery of Quadric Surfaces
- Previous: The hyperboloid of one sheet