Cross sections of a surface
In general, the graph of an equation involving three variables is a surface that is floating in three dimensions. If one can write the equation in the form $z=f(x,y)$, then the surface is the graph of the function $f(x,y)$. Otherwise, the surface can be viewed as being defined implicitly from the equation.
Unfortunately, the plot of a surface in three dimensions is more difficult to draw and visualize that plots of curves in two dimensions. We can often get insight into a surface by making a series of plots of curves in two dimensions. One way to do this is to plot level curves. If the surface is the graph of a function $z=f(x,y)$, then by fixing the variable $z$ to a single value $z=c$, one obtains a level curve of the function $c=f(x,y)$.
Cross sections are generalizations of level curves to holding any one of the three variables $x$, $y$, or $z$ fixed. One can take cross sections of surfaces defined implicitly as well as graphs of functions. We often refer to the cross sections where $z$ is fixed as horizontal cross sections (for graphs of functions, we can call them level curves). We often refer to cross sections where either $x$ or $y$ is fixed as vertical cross sections.
For example, consider the following equation of a sphere of radius 2: $$x^2 + y^2 + z^2= 4.$$ To examine a cross section, we choose a value for one of the three variables, say $z=0$. Using that value, we take a look at the resulting new equation: $$x^2 + y^2 + 0^2 = 4, \qquad \text{or} \qquad x^2 + y^2 = 4.$$
You should recognize this as a circle of radius 2, centered at the point $(x,y)=(0,0)$. In other words, the intersection of the plane $z=0$ and the sphere $x^2 + y^2 + z^2 = 4$ is a circle of radius 2. A more intuitive way to think about this is that you take a big meat cleaver and chop the sphere where $z=0$. If you take one of the resulting half-spheres, what does the edge look like? A circle of radius two.
The below picture is an illustration of this cross section. You can see where the plane $z=0$ slices through the sphere.
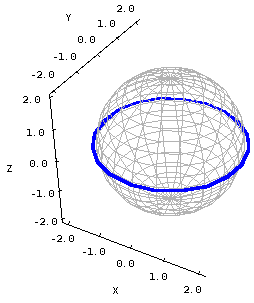
Cross section of a sphere. The blue curve on the sphere illustrates the cross section $z=0$ on the unit sphere $x^2+y^2+z^2=0$. This cross section is a circle $x^2+y^2=1$.
This method can help you figure out what surfaces look like. It is particularly nice for the quadric surfaces, as the cross sections are all familar conic sections. When you put together the cross sections for $x$, $y$, and $z$, you develop a picture of the surface.
Thread navigation
Interactive Gallery of Quadric Surfaces
- Previous: Quadric surfaces
- Next: The elliptic paraboloid