Surfaces defined implicitly
Implicit curves
A graph of a scalar-valued function of a single variable, $y=f(x)$, is a curve. Graph the equation $y=f(x)$ is easy because the value of $y$ is given explicitly for each value of $x$. Even if we aren't told what the function is, we can easily graph an equation such as $y=(x-1)^2$ since it is solved explicitly for $y$.
Sometimes, however, we want to graph an equation such as the equation $x^2+y^2=1$. You might recall that equations like these are called implicit functions, because we can't explicitly solve for $y$ in terms of $x$. If you try to solve this equation for $y$, you get $y = \pm \sqrt{1-x^2}$. The graph of such an equation is still well defined. It is the set of points $(x,y)$ where $x^2+y^2=1$, which is the circle of radius one centered at the origin.
Implicit surfaces
We can also graph equations in terms of three variables, say $x$, $y$, and $z$. Sometimes, we can solve the equation explicitly in terms of $z$ and write it as $z=f(x,y)$. In this case, we've reduced the problem to the graph of a scalar-function of two variables, which is a surface.
On the other hand, we cannot solve an equation like $x^2+y^2+z^2=1$ explicitly for $z$. Even so, the equation still implicitly defines a surface. The surface, i.e., the graph of the equation, is the set of points $(x,y,z)$ that satisfy $x^2+y^2+z^2=1$. These points form a sphere of radius one centered at the origin.
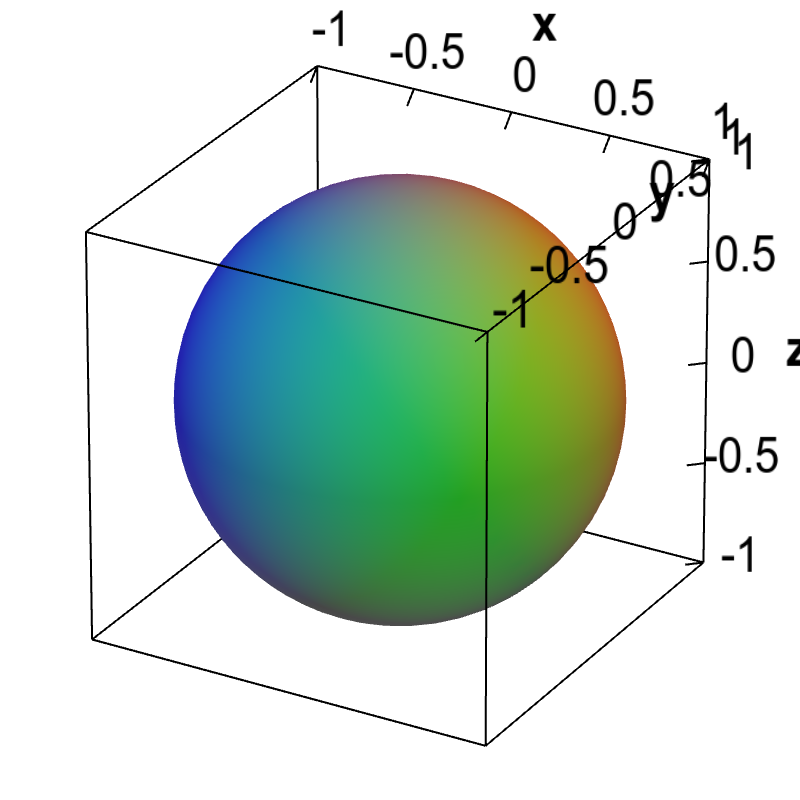
Applet loading
A spherical implicit surface. The graph of the equation $x^2+y^2+z^2=1$ is the unit sphere centered at the origin.
For additional examples of implicit surfaces, look at the quadric surfaces, many of which are defined implicitly. In addition, the level surfaces used to visualize the functions of three variables are generally implicit surfaces.